Max Lloyed Quantizer
In this case quantizers are designed minimizing MSQE and tables are developed for input governed by standard distribution functions such as gamma, Laplacian, Gaussian, Rayleigh, Uniform. Quantizers can also be designed tailored to histograms. For a well designed predictor, the histrogram of predicted errors tend to follow Laplacian distribution.
Given the range of input f as from 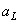 to to 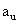 , and the number of output levels as J, we design the quantizer s.t MSQE is minimum. , and the number of output levels as J, we design the quantizer s.t MSQE is minimum.
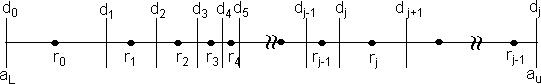
Figure (3.3.3)
Let 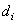 = decision level ( = decision level ( 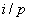 level) level)
and 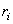 = reconst level ( = reconst level ( 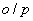 level) level)
This is shown in the above figure (3.3.3).
If 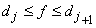 then then 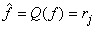 and and
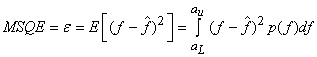
where 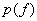 = Probability density function of random variable f = Probability density function of random variable f
The error 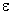 can also be written as can also be written as
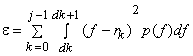
 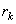 and and 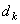 are variables. To minimize are variables. To minimize 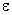 we set we set 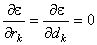
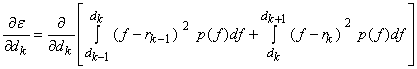
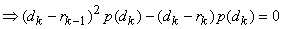
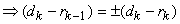
Since 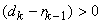 and and 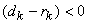 solution that is valid is solution that is valid is
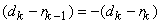
or
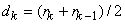
i.e. input level is average of two adjacent output levels. Also
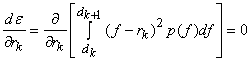
or , 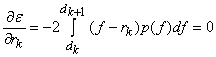
Hence
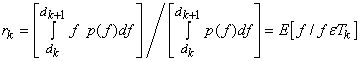
where 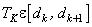
Output level is the centroid of adjacent input levels. This solution is not closed form. To find input level 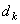 , one has to find , one has to find 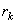 and vice versa. However by iterative techniques both and vice versa. However by iterative techniques both 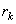 and and 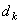 can be found using Newton 's method. can be found using Newton 's method.
When number of output levels 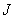 s large, the quantizer design can be approximated as follows: Assuming s large, the quantizer design can be approximated as follows: Assuming 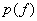 is constant over each quantization level, or a piecewise constant function is constant over each quantization level, or a piecewise constant function
As shown in Figure (3.7), we have, a 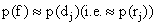 ; ;
We have, 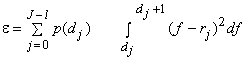
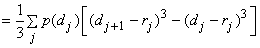
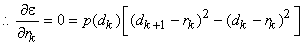
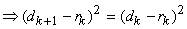
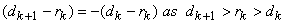
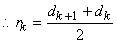
i.e. each reconstruction level lies mid-way between two adjacent decision levels. |