Color Transformations
Many situations arise in the application of colorimetry where it is required to compute the tristimulus values of a color in terms of a second set of primaries when these values are known in terms of a first set of primaries. Such transformations allow comparison of result obtained with different colorimeters, for example. Also, in color television such transformations are very useful since the spectral characteristics of the camera may be quite different from the primaries used by the television receiver. The problem then can be stated as follows:
Given the tristimulus value 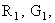 and and 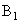 of some specific color in terms of one set of primaries, derive the tristimulus values
of some specific color in terms of one set of primaries, derive the tristimulus values
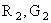 and
and
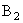 of the same color in terms of the second set of primaries.
of the same color in terms of the second set of primaries.
Obviously, in order to derive the transformation, the second set of primaries and the reference white must be completely specified in terms of the first set of primaries. We assume in the following that the reference white is the same equal energy white E for both sets of primaries. As an example, we treat the problem of transforming between the two primary systems
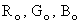 and X,Y,Z. and X,Y,Z.
Let us represent the (x,y,z) chromaticity coordinates of primaries 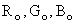 by
by
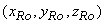 , ,
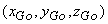 and and
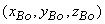 respectively. Also let respectively. Also let
m 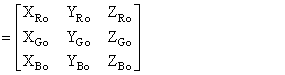 |
(2.2) |
Similarly, let the (X, Y, Z) tristimulus values of the primaries 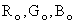 be represented by
be represented by 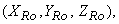 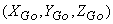 and
and
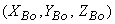 respectively. Also, let respectively. Also, let
M 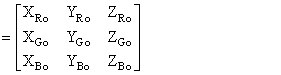 |
(2.3) |
By definition of tristimulus values,
R0 =XRo X + YRo Y + ZRo Z
G0 =XGo X + YGo Y + ZGo Z
B0 =XBo X + YBo Y + ZBo Z
|
(2.4) |
or in matrix notaion
 |
(2.5) |
For an arbitrary color stimulus C, having tristimulus values
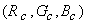 and and
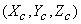 with respect to primaries with respect to primaries
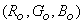 and (X,Y,Z), respectively, the following is true: and (X,Y,Z), respectively, the following is true:
| C = Rc Ro + Gc Go +Bc B o = Xc X + Yc Y +Zc Z |
(2.6) |
|