Color Mixtures
One important objective of colorimetry is to be able to specify the color of a mixture in terms of the components of the mixture. We have already seen that the experimentally observed Grassman's laws state that the tristimulus values of a color mixture are obtained by vector addition of the tristumulus values of the components of the mixture. Thus, if colors 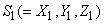 and and 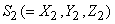 are mixed to obtain
color are mixed to obtain
color
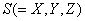 , then , then
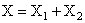
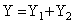
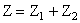
However, the chromaticities (x,y,z) do not simply add. Thus, we would like to obtain similar equations for the chromaticity-luminance coordinates of he mixture S(x,y,Y) obtained from the colors
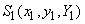 and and
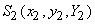 Using the relationship between tristumulus values and chromaticity coordinates, we get Using the relationship between tristumulus values and chromaticity coordinates, we get
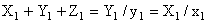
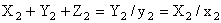
Adding both sides and using Eq.(1.8.13)
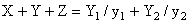
Thus
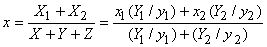
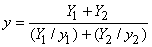
and
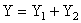 Similar results can be obtained for other sets of chromaticity coordinates such as
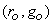 . We see that the chromaticity coordinates of the mixture are obtained by a weighted linear sum of the chromaticity coordinates of the components of the mixture. This means that if we mix two colors having chromaticities . We see that the chromaticity coordinates of the mixture are obtained by a weighted linear sum of the chromaticity coordinates of the components of the mixture. This means that if we mix two colors having chromaticities
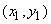 and and
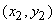 then the chromaticity of the mixture will lie on the straight line connecting the points then the chromaticity of the mixture will lie on the straight line connecting the points
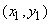 ; and ; and 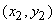 . The exact location on the straight line will be determined by the luminances . The exact location on the straight line will be determined by the luminances 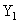 and and 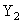 . .
Figure( 2.15) Dominant wavelength (point D,605 nm) for color S1 and complementary wavelength ( point D' , 496 nm) for color S2
This is shown in Fig. 2.15, where the chromaticity of a mixture of colors 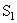 and and 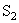 lies on the straight lies on the straight 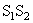 .Carrying this further, consider the three primary colors .Carrying this further, consider the three primary colors 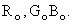 We see that the chromaticities of all possible (positive) mixtures of the three primary colors We see that the chromaticities of all possible (positive) mixtures of the three primary colors 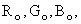 whose chromaticity coordinates are plotted in Fig 2.13 at (0,0,), (1,0), (0,1), will lie within the triangle having those vertices. We see, therefore, that there is a large range of spectral colors that cannot be synthesized by nonnegative amounts of primaries whose chromaticity coordinates are plotted in Fig 2.13 at (0,0,), (1,0), (0,1), will lie within the triangle having those vertices. We see, therefore, that there is a large range of spectral colors that cannot be synthesized by nonnegative amounts of primaries 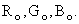 On the other hand, in the (x,y) chromaticity diagram of Fig 2.13 all the spectral colors, including the line of purples, lie within the triangle with vertices (0,0), (1,0) and (0,1) and, therefore, all real colors can be synthesized by positive amounts of the X,Y,Z primary colors. All three vertices are, however, outside the spectral locus, thus making them nonreal. This illustrates two of our previous statements: (a)Negative amounts of a primary in the On the other hand, in the (x,y) chromaticity diagram of Fig 2.13 all the spectral colors, including the line of purples, lie within the triangle with vertices (0,0), (1,0) and (0,1) and, therefore, all real colors can be synthesized by positive amounts of the X,Y,Z primary colors. All three vertices are, however, outside the spectral locus, thus making them nonreal. This illustrates two of our previous statements: (a)Negative amounts of a primary in the 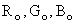 system may be required for a color match; (b) All real colors can be matched by positive amounts of primary colors X,Y,Z. However, the primary colors themselves are nonreal. system may be required for a color match; (b) All real colors can be matched by positive amounts of primary colors X,Y,Z. However, the primary colors themselves are nonreal.
|