Introduction

Concept of Visual Information

The ability to see is one of the truly remarkable characteristics of living beings. It enables them to perceive and assimilate in a short span of time an incredible amount of knowledge about the world around them. The scope and variety of that which can pass through the eye and be interpreted by the brain is nothing short of astounding.

It is thus with some degree of trepidation that we introduce the concept of visual information, because in the broadest sense, the overall significance of the term is overwhelming. Instead of taking into account all of the ramifications of visual information; the first restriction we shall impose is that of finite image size, In other words, the viewer receives his or her visual information as if looking through a rectangular window of finite dimensions. This assumption is usually necessary in dealing with real world systems such as cameras, microscopes and telescopes for example; they all have finite fields of view and can handle only finite amounts of information.

The second assumption we make is that the viewer is incapable of depth perception on his own. That is, in the scene being viewed he cannot tell how far away objects are by the normal use of binocular vision or by changing the focus of his eyes.

In this setup, the visual information is determined completely by the wavelengths and amplitudes of light that passes through each point of the window and reach the viewers eye. If the world outside were to be removed and a projector installed that reproduced exactly the light distribution on the window, the viewer inside would not be able to tell the difference.

Thus, the problem of numerically representing visual information is reduced to that of representing the distribution of light energy and wavelengths on the finite area of the window. We assume that the image perceived is "monochromatic" and static. It is determined completely by the perceived light energy (weighted sum of energy at perceivable wavelengths) passing through each point on the window and reaching the viewer's eye. If we impose Cartesian coordinates on the window, we can represent perceived light energy or "intensity" at point by 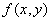. Thus 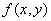represents the monochromatic visual information or "image" at the instant of time under consideration. As images that occur in real life situations cannot be exactly specified with a finite amount of numerical data, an approximation of 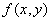must be made if it is to be dealt with by practical systems. Since number bases can be changed without loss of information, we may assume to be represented by binary digital data. In this form the data is most suitable for several applications such as transmission via digital communications facilities, storage within digital memory media or processing by computer.