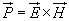The left hand side of equation (6.36) can be written as where (W/mt²) is called the Poynting vector and it represents the power density vector associated with the electromagnetic field. The integration of the Poynting vector over any closed surface gives the net power flowing out of the surface. Equation (6.36) is referred to as Poynting theorem and it states that the net power flowing out of a given volume is equal to the time rate of decrease in the energy stored within the volume minus the conduction losses.

Poynting vector for the time harmonic case:

For time harmonic case, the time variation is of the form , and we have seen that instantaneous value of a quantity is the real part of the product of a phasor quantity and when is used as reference. For example, if we consider the phasor