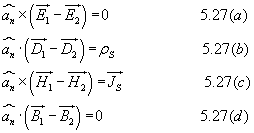Boundary Conditions for Electromagnetic fields

The differential forms of Maxwell's equations are used to solve for the field vectors provided the field quantities are single valued, bounded and continuous. At the media boundaries, the field vectors are discontinuous and their behaviors across the boundaries are governed by boundary conditions. The integral equations(eqn 5.26) are assumed to hold for regions containing discontinuous media.Boundary conditions can be derived by applying the Maxwell's equations in the integral form to small regions at the interface of the two media. The procedure is similar to those used for obtaining boundary conditions for static electric fields (chapter 2) and static magnetic fields (chapter 4). The boundary conditions are summarized as follows

With reference to fig 5.3