We now introduce the vector magnetic potential which can be used in regions where current density may be zero or nonzero and the same can be easily extended to time varying cases. The use of vector magnetic potential provides elegant ways of solving EM field problems.

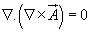Since and we have the vector identity that for any vector , , we can write .

Here, the vector field is called the vector magnetic potential. Its SI unit is Wb/m. Thus if can find of a given current distribution, can be found from through a curl operation.

We have introduced the vector function and related its curl to . A vector function is defined fully in terms of its curl as well as divergence. The choice of 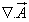is made as follows.

 ...........................................(4.24)

By using vector identity, .................................................(4.25)

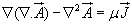   .........................................(4.26)