When this expression is integrated over the source region, we get the electric field at the point P due to this distribution of charges. Thus the expression for the electric field at P can be written as:

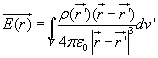..........................................(2.8)

Similar technique can be adopted when the charge distribution is in the form of a line charge density or a surface charge density.

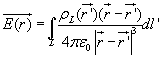........................................(2.9)

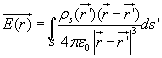........................................(2.10)

Electric flux density:

As stated earlier electric field intensity or simply ‘Electric field' gives the strength of the field at a particular point. The electric field depends on the material media in which the field is being considered. The flux density vector is defined to be independent of the material media (as we'll see that it relates to the charge that is producing it).For a linear