From the foregoing discussions we observe that the electric field strength at any point is the negative of the potential gradient at any point, negative sign shows that 
is directed from higher to lower values of 
. This gives us another method of computing the electric field, i. e. if we know the potential function, the electric field may be computed. We may note here that that one scalar function contain all the information that three components of carry, the same is possible because of the fact that three components of are interrelated by the relation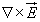 
.
Example: Electric Dipole
An electric dipole consists of two point charges of equal magnitude but of opposite sign and separated by a small distance.
As shown in figure 2.11, the dipole is formed by the two point charges Q and -Q separated by a distance d , the charges being placed symmetrically about the origin. Let us consider a point P at a distance r, where we are interested to find the field.
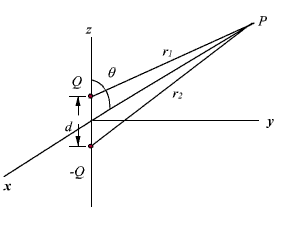
Fig 2.11 : Electric Dipole