Electrostatic Potential and Equipotential Surfaces

In the previous sections we have seen how the electric field intensity due to a charge or a charge distribution can be found using Coulomb's law or Gauss's law. Since a charge placed in the vicinity of another charge (or in other words in the field of other charge) experiences a force, the movement of the charge represents energy exchange. Electrostatic potential is related to the work done in carrying a charge from one point to the other in the presence of an electric field.

Let us suppose that we wish to move a positive test charge from a point P to another point Q as shown in the Fig. 2.8.

The force at any point along its path would cause the particle to accelerate and move it out of the region if unconstrained. Since we are dealing with an electrostatic case, a force equal to the negative of that acting on the charge is to be applied while moves from P to Q. The work done by this external agent in moving the charge by a distance is given by:

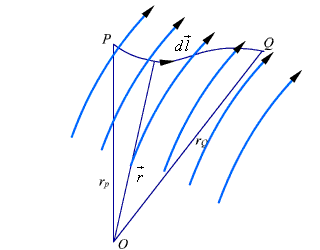
Fig 2.8: Movement of Test Charge in Electric Field

.............................(2.23)