Co-ordinate Systems

In order to describe the spatial variations of the quantities, we require using appropriate co-ordinate system. A point or vector can be represented in a curvilinear coordinate system that may be orthogonal or non-orthogonal .

An orthogonal system is one in which the co-ordinates are mutually perpendicular. Non-orthogonal co-ordinate systems are also possible, but their usage is very limited in practice .

Let u = constant, v = constant and w = constant represent surfaces in a coordinate system, the surfaces may be curved surfaces in general. Furthur, let , and be the unit vectors in the three coordinate directions(base vectors). In a general right handed orthogonal curvilinear systems, the vectors satisfy the following relations :

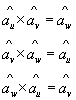.....................................(1.13)

These equations are not independent and specification of one will automatically imply the other two. Furthermore, the following relations hold