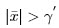The Bayesian approach to composite hypothesis testing discussed earlier suffers from following limitations:

• In some cases, it is not obvious how to assign the prior probability of the hypotheses.
• If both the hypotheses contain unknown parameters, finding the Bayesian solution becomes very tedious and often the involved integrals do not yield closed-form solution.

On account of the above limitations, one can use an alternative hypothesis testing approach referred to as generalized likelihood ratio test (GLRT) and is presented in the following.

8.8.1 Generalized Likelihood Ratio Test (GLRT)

In this approach, the unknown parameters are first estimated from the observed data under either or both the hypotheses. In the GLRT, the unknown parameters are replaced by their maximum likelihood estimate (MLE) in the likelihood ratio. Although there is no optimality associated with the GLRT, in practice, it appears to work quite well. In general a GLRT decides 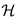₁ if:

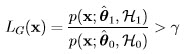
where 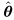₁ is the MLE of θ₁ assuming 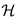₁ is true (i.e., maximizes p(x; 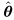₁)), and 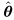₀ is the MLE of θ₀ assuming 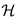₀ is true (i.e., maximizes p(x; 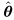₀)). This approach also provides information about the unknown parameters since the first step in determining L_G(x) is to find the MLEs.

8.7.3 Example

8.7.3 Example

Detection of the unknown DC level in WGN: GLRT approach

Assume θ₁ = A and there is no unknown parameters under ₀. The hypothesis test becomes,

Thus the GLRT decides ₁ if

The MLE of A is found by maximizing

and that is well known to be  = . Thus,

On taking logarithm of both sides, we have

or GLRT decides ₁ if

Remark: Note the form of the detector is the identical to that has been obtained using the Bayesian approach. The derivation of the detector using GLRT often turns out to be much simpler than that of Bayesian approach.

8.8.3 Summary of Parametric Detectors

The salient attributes of the different parametric detection approaches discussed in this module are summaried as below:

• The Bayesian detector is the most general detector which not only accounts for the prior probability of the hypotheses but also the costs of each of the decisions made. It minimizes the average cost or risk in a decision making.


• The minimax detector is a variant of the Bayesian detector which accounts for the uncertainity about choosing the prior probability. It minimizes the worst case average cost in a decision making.


• The Nayman-Pearson (NP) detector is the well-known classical detector which optimizes the detection probability given a fixed level of false alarm probability. It is based on the observed data only and does not require any prior information about the hypotheses. As a result of this it can be applied in alomost all detection problems.


• In contrast to simple hypothesis testing where the PDFs under all hypotheses is completely known, the composite hypothesis testing where one or more hypothses have unknown parameter(s) is much more challenging.


• In the Bayesian approach to composite hypothesis testing, the likelihood ratio test is performed by integrating out the unknown parameter(s) using its prior PDF. This approach yields optimal detector but in general it does not lead to closed-form derivation of the detector.


• The generalized likelihood ratio test (GLRT) forms the most commonly used approach for the composite hypothesis testing. In this appraoch, the unknown parameter is substituted with its the maximum likelihood estimate (MLE) obtained from the observed data to perform the likelihood ratio test. The GLRT approach is very effective in practice though the optimality of the resulting detector is not guaranteed in all cases.