4.2.1 Basic Procedure of MLE
In some case the MVUE may not exist or it cannot be found by any of the methods discussed so far. The maximum likelihood estimation (MLE) approach is an alternative method in cases where the PDF or the PMF is known. This PDF or PMF involves the unknown parameter θ and is called the likelihood function. With MLE the unknown parameter is estimated by maximizing the likelihood function for the observed data. The MLE is defined as:
where x is the vector of observed data (of N samples).
It can be shown that 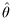 is asymptotically unbiased:
is asymptotically unbiased:
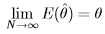
and asymptotically efficient:
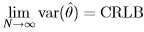
An important result is that if an MVUE exists, then the MLE procedure will produce it.
Proof
Assume a scaler parameter case, if an MVUE exists, then the log-likelihood function can be factorized as
![x [n ] = A + w[n] n = 0,1,...,N - 1](images/5.jpg)
where 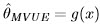 .
.
On maximizing the likelihood function, by setting its derivative to zero, yields the MLE
![[ N-1 ] ---1---- 1--∑ 2 p(x; θ) = (2πθ)N2 exp - 2θ (x[n] - θ) n=0](images/7.jpg)
Another important observation is that unlike the previous estimates the MLE does not require an explicit expression for p(x; θ)! Indeed given a histogram plot of the PDF as a function of θ one can numerically search for the θ that maximizes the PDF.
4.2.2 Example
Consider the problem of a DC signal embedded in noise:
![x [n ] = A + w[n] n = 0,1,...,N - 1](images/8.jpg)
where w[n] is WGN with zero mean and known variance σ2.
We know that the MVU estimator for θ is the sample-mean. To see that this is also the MLE, we consider the PDF:
![[ N-1 ] ---1---- 1--∑ 2 p(x; θ) = (2πθ)N2 exp - 2θ (x[n] - θ) n=0](images/9.jpg)
and maximize the log likelihood function by setting it to zero:
![( ) 1 1 N∑ -1 2 lnp (x; θ) = ln ------N- - --- (x [n ] - θ) (2πθ )2 2θ n=0](images/10.jpg)
Thus 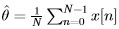 which is the sample-mean.
which is the sample-mean.
4.2.3 Example
Consider the problem of a DC signal embedded in noise:
![x [n ] = A + w[n] n = 0,1,...,N - 1](images/12.jpg)
where w[n] is WGN with zero mean but unknown variance which is also A, that is the unknown parameter, θ = A, manifests itself both as the unknown signal and the variance of the noise. Although a highly unlikely scenario, this simple example demonstrates the power of the MLE approach since finding the MVUE by the procedures is not easy. Consider the likelihood function for x is given by:
![[ N-1 ] ---1----- -1--∑ 2 p(x; θ) = (2πσ2)N2 exp - 2σ2 (x[n] - θ) n=0](images/13.jpg)
Now consider p(x; θ) as a function of θ, thus it is a likelihood function and we need to maximize it with respect to θ. For Gaussian PDFs it is easier to find the maximum of the log-likelihood function (since logarithm is a monotonic function):
![∂ lnp(x; θ) 1 N∑- 1 N∑- 1 -----------= --- (x [n] - θ) = 0 ⇒ (x [n ] - N θ) = 0 ∂θ σ2 n=0 n=0](images/14.jpg)
On differentiating we have:
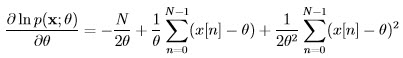
on setting the derivative to zero and solving for θ, produces the MLE:
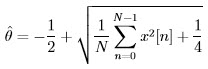
where we have assumed θ > 0. It can be shown that:
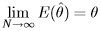
and:
 is asymptotically unbiased:
is asymptotically unbiased:
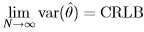
![x [n ] = A + w[n] n = 0,1,...,N - 1](images/5.jpg)
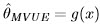 .
.![[ N-1 ] ---1---- 1--∑ 2 p(x; θ) = (2πθ)N2 exp - 2θ (x[n] - θ) n=0](images/7.jpg)
![x [n ] = A + w[n] n = 0,1,...,N - 1](images/8.jpg)
![[ N-1 ] ---1---- 1--∑ 2 p(x; θ) = (2πθ)N2 exp - 2θ (x[n] - θ) n=0](images/9.jpg)
![( ) 1 1 N∑ -1 2 lnp (x; θ) = ln ------N- - --- (x [n ] - θ) (2πθ )2 2θ n=0](images/10.jpg)
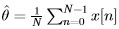 which is the sample-mean.
which is the sample-mean.![x [n ] = A + w[n] n = 0,1,...,N - 1](images/12.jpg)
![[ N-1 ] ---1----- -1--∑ 2 p(x; θ) = (2πσ2)N2 exp - 2σ2 (x[n] - θ) n=0](images/13.jpg)
![∂ lnp(x; θ) 1 N∑- 1 N∑- 1 -----------= --- (x [n] - θ) = 0 ⇒ (x [n ] - N θ) = 0 ∂θ σ2 n=0 n=0](images/14.jpg)