Solution 4
(a) The difference equation describing a causal LTI system is given by
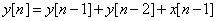
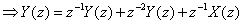
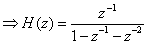
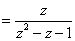
From the system function, we can see that the poles of the system are at
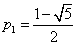 and and 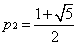 . Since the system is given to be causal, the ROC . Since the system is given to be causal, the ROC
is 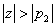 . Figure gives the pole-zero plot for this system. . Figure gives the pole-zero plot for this system.
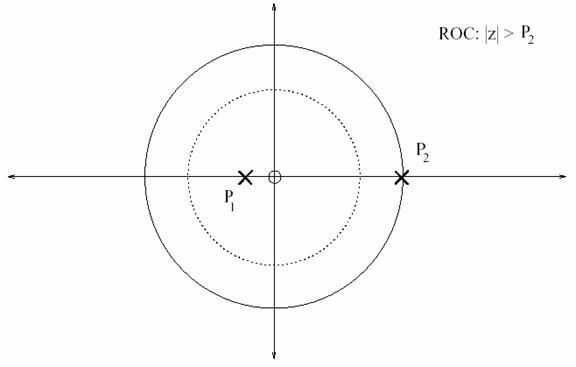
Figure: Pole-zero plot of H ( z ). The dotted line represents the unit circle.The ROC is outside the bigger circle. NOTE : Since the ROC doesn't contain the unit circle, the system is NOT stable.

(b) We can write H ( z ) using a partial fraction expansion as
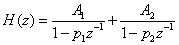 , , 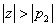
for constants given by 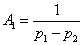 , , 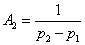 . Taking the Inverse Z-transform of H(z) , we get . Taking the Inverse Z-transform of H(z) , we get
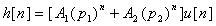
(c) Since 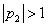 ,
it is clear that the impulse response found in part (b) is unstable.
For the system to be stable, the ROC must include the unit circle.
Hence the ROC we need to consider is ,
it is clear that the impulse response found in part (b) is unstable.
For the system to be stable, the ROC must include the unit circle.
Hence the ROC we need to consider is 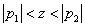 . For this ROC, the impulse response will be given by . For this ROC, the impulse response will be given by
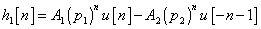 
|