| Solution 7
From Sampling Theorem we know that if 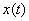 be a band-limited signal with be a band-limited signal with
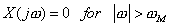 , then , then 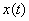 is uniquely determined by its samples is uniquely determined by its samples
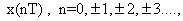 if if
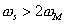 , ,
where
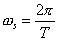
Now,
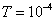
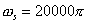
(a) 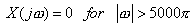
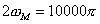
Here, obviously, 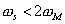 . .
Hence 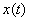 can be recovered exactly from can be recovered exactly from 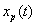 . .

(b) 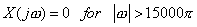
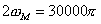
Here, obviously 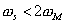 , ,
Hence 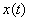 can be recovered exactly from can be recovered exactly from 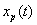 . .

(c) 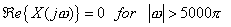
Real part of 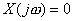 , but we can't say anything particular about imaginary part of the , but we can't say anything particular about imaginary part of the 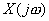 , thus not necessary that , thus not necessary that 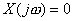 for this particular range. for this particular range.
Hence 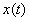 cannot be recovered exactly from cannot be recovered exactly from 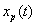 . .

(d) 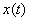 real and real and 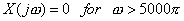
As 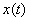 is real we have is real we have 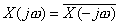
Taking mod on both sides
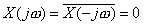 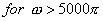
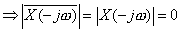 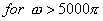
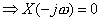 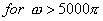
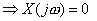 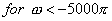
So, we get
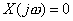 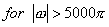
Here , obviously 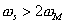 , ,
Hence x(t) can be recovered exactly from 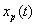 . .

(e) 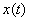 real and real and 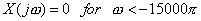
Proceeding as above we get
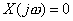 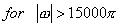
Here, obviously 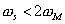 , ,
Hence x(t) cannot be recovered exactly from 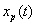 . .

(f) 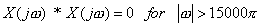
When we convolve two functions with domain 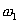 to to 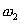 and and 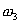 to to 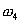 then the domain of their convolution function varies from then the domain of their convolution function varies from 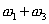 to to 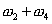 . .
Here, 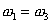 and and 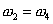
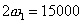
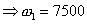
Therefore,
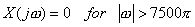
Here, obviously 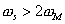 , ,
Hence x(t) can be recovered exactly from 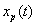 . .

(g) 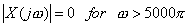
We cannot say anything about 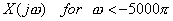 , ,
Hence x(t) cannot be recovered exactly from 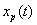 . .

|