Solution 8
(1)
(a)
It is periodic with period 2. So, consider segment between 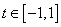 . .
Let
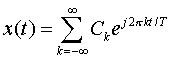
be the Fourier expansion, where:
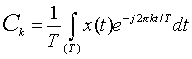
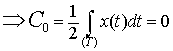
For 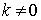 , ,
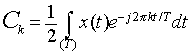
But, 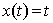 in in 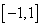
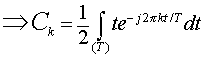
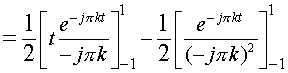
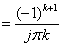

Substituting in x(t) 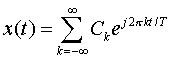
(b)
It is periodic with period 6. So, consider segment between 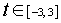 . .
The function in this interval is:
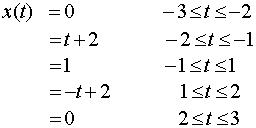
Let
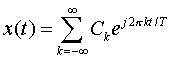
be the Fourier expansion, where:
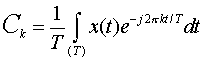
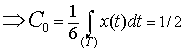
For 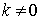 , ,
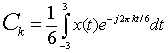
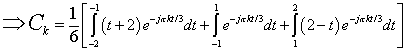
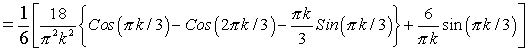
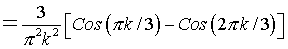

Substituting in x(t)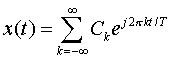
(c)
It is periodic with period 3, so take the segment 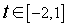
The function in the interval is:
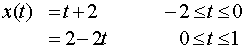
Let
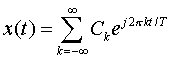
be the Fourier expansion, where:
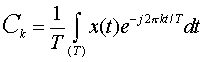
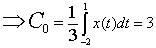
For 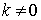 , ,
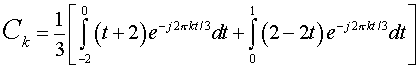
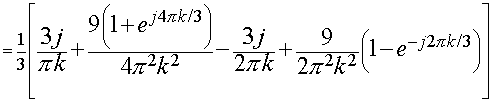
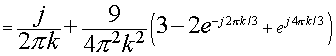

Substituting in x(t)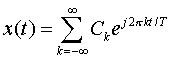
(d)
It is periodic with period 2. So take segment 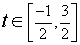
Here,
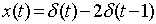
Let
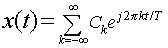
be the Fourier expansion, where:
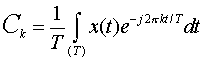
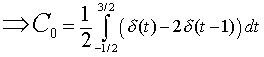
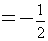
For 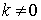
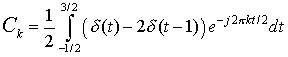
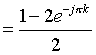

Substituting in x(t)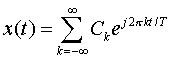
(e)
It is periodic with period 6. So, take the segment 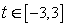
Here 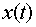 will be will be
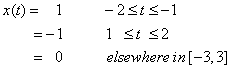
Let
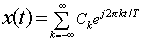
be the Fourier expansion, where:
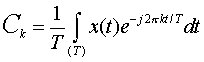
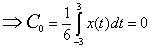
For 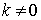
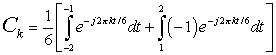
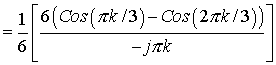
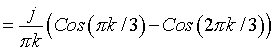

Substituting in x(t)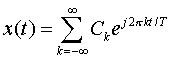
(f)
It is periodic with period 3. So, take the segment 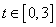
Here 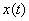 will be will be
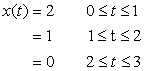
Let
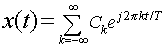
be the Fourier expansion, where:
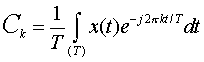
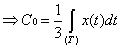
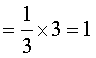
For 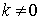
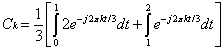
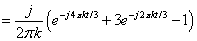
Substituting in x(t)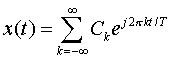

Substituting in x(t) 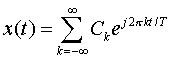
(2) Let 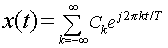
be the Fourier expansion, where:
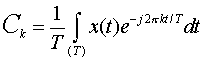
Given 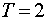 . .
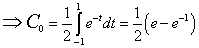
For 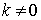
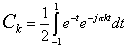
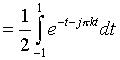
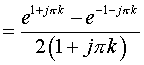
Substituting in x(t) 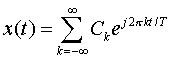

(3) Let
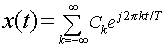
be the Fourier expansion, where:
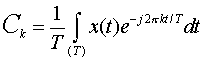
Given 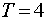 . .
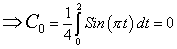
For 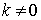
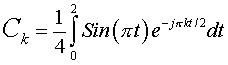
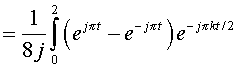
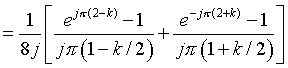
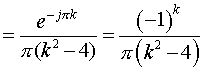
Substituting in x(t) 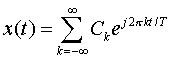

|