Solution 2
Since 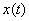 is a real signal, is a real signal, 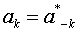 . But from the given hypothesis, . But from the given hypothesis, 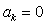 for k > 2. This implies that for k > 2. This implies that 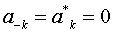 for k > 2.
Also, it is given that
for k > 2.
Also, it is given that 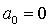 . Therefore the only non-zero Fourier coefficients are . Therefore the only non-zero Fourier coefficients are 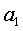 , , 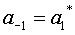 , , 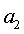 and and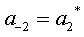 .
It is also given that .
It is also given that 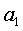 is a positive real number. Therefore is a positive real number. Therefore 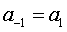 . Thus we have, . Thus we have,
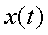 = = 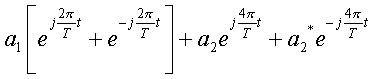
= 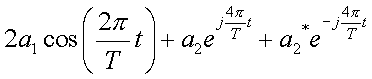
= 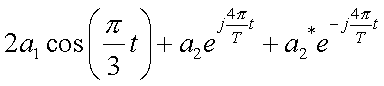
Since 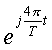 and and 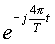 are both periodic with period 3, we have are both periodic with period 3, we have
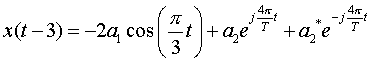
But, by given hypothesis we have 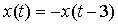 , which implies that , which implies that
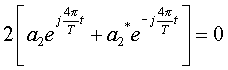
Therefore we have,
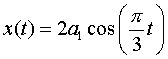
Finally, it is given that
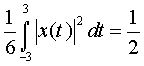
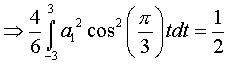
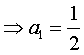
Therefore, 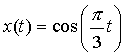 and the constants A = 1, B = and the constants A = 1, B = 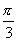 and C = 0. and C = 0.

|