| Solution 6
(a) Consider the signal 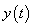 shown below. shown below.
Fig. (a)
Now consider convolution of  with itself. Let the resultant signal be with itself. Let the resultant signal be  . .
Then, 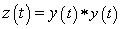 . .
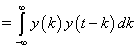
Now, consider 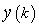 and and 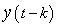 . .
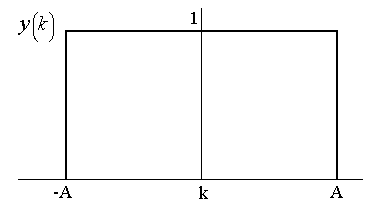
Fig (b)
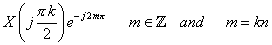
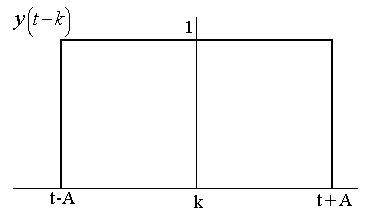
Fig (c)
So, when  . .
 as there is no overlap between as there is no overlap between 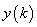 and and 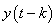 . .
When  . .
Then, 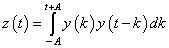 . .
Here, 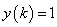 and and 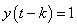 . .
So, 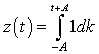 . .
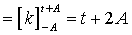 . .
When  . .
Then, there is no overlap between 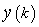 and and 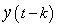 . .
So, the signal  is is
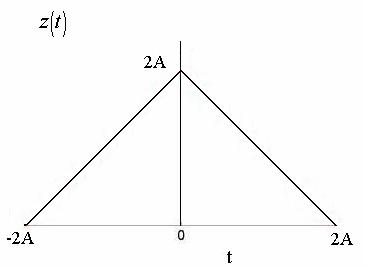
Fig. (d)
Now compare 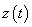 with the given signal with the given signal 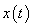 . Here . Here  is is
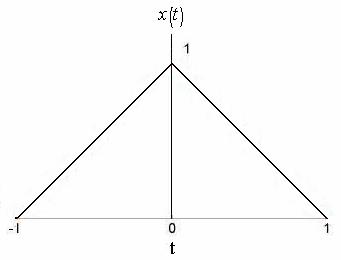
Fig. (e)
By comparing, we get 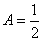 . .
So, 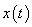 can be thought of as a signal which is a convolution of the signal can be thought of as a signal which is a convolution of the signal 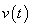 with itself, where with itself, where 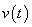 is is
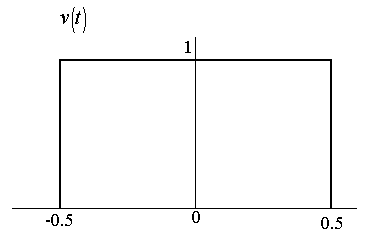
Fig. (f)
This implies 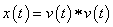 . .
By Convolution Theorem, the Fourier Transform of 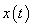 is square of the Fourier Transform of is square of the Fourier Transform of 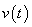 , i.e. , i.e. 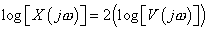 . .
Now, consider 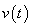 . Its Fourier Transform . Its Fourier Transform 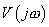 is is
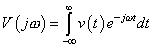
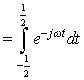
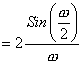 . .
So, 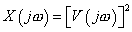
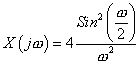 . . 
(b) 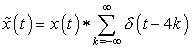
Now, consider a signal 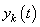 , where , where
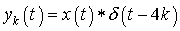
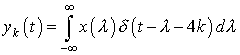
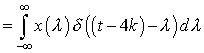
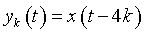 as as 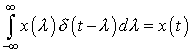 . .
So, 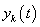 is the shifted version of is the shifted version of 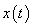 by 4k along the t axis which is shown as by 4k along the t axis which is shown as
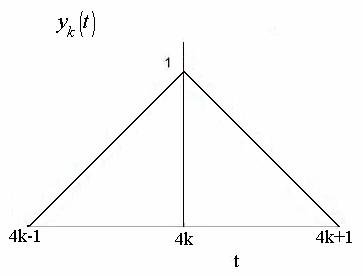
Fig. (g)
Now, 
So,  is is
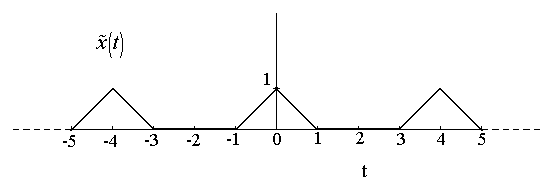
Fig. (h) 
(c) Any signal which is the shifted version of 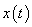 by 4k on the t axis can be taken as by 4k on the t axis can be taken as 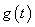 , which satisfies , which satisfies 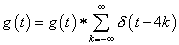 because by the last part we can say that when we convolve because by the last part we can say that when we convolve 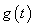 with with 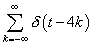 , it will result in , it will result in 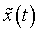 . .
In this case, 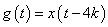 , where , where 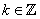 . .
(d) By part (c) ,
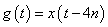 , where , where 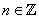 . .
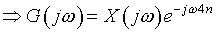 . .
Now, put 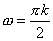 . .
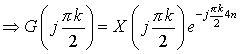
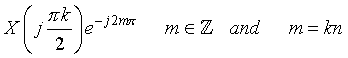
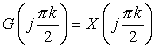 as as 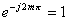 
|