|
Solution 8 :
By definition ;
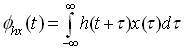
Replacing x (t) by cx(t) where c is a real
number ,
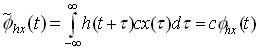
Similarly putting ,
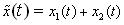 , we get
, we get
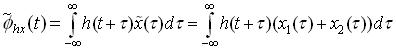
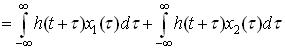
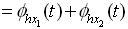
Thus ,
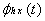 obeys homogeneity and additivity .
obeys homogeneity and additivity .
Implies
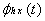 is LINEAR .
is LINEAR .
NEXT , substituting x (t) by x (t-t0)
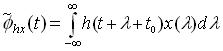
Now , Substituting ,
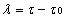 ,we get
,we get
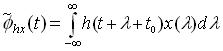
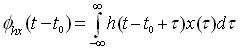
Hence
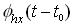 need not be equal to
need not be equal to
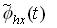 for all x (t) and t0.
for all x (t) and t0.
Hence
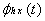 is shift-variant .
is shift-variant .
Let
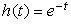 and let x (t) = u (t) and let x (t) = u (t)
Now ,
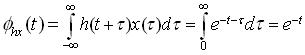
Even though x (t)=0 for t < 0 ,
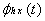 is non-zero for t < 0 .
is non-zero for t < 0 .
This counterexample shows
that the auto correlating
system is non-causal.
(b) The system remains linear
(homogeneous and additive) and non-causal. The system
becomes shift invariant.
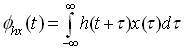
Replacing x (t) by x (t-t0) , we get
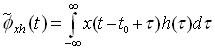 and
and
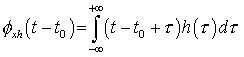
Hence
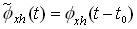 for all signals x (t) and all values of t0
.
for all signals x (t) and all values of t0
.
Thus
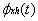 is a shift-invariant system .
is a shift-invariant system .
|