Solution 2
(a) True
Proof: For a system to be stable
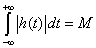 ; ; 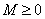
If h is periodic with period P (say), then
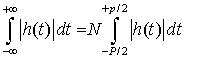 (where (where 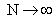 ) )
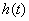 is non-zero is non-zero
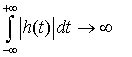
Hence unstable.
(b) False
Counter example :
Let an LTI system 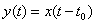
Or
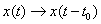
Which is causal
For its inverse system, 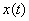 will be output and will be output and 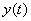 will be input. will be input.
i.e. 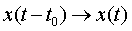
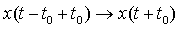 [Using shift invariance] [Using shift invariance]
Which is non-causal.
(c) False
Counter example :
Let 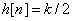 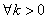
Here
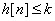 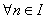
But
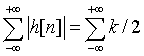
Which is not bounded.
Hence , the impulse response must be absolutely summable , for the system to be stable.
(d) False
Counter example :
Let
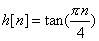 for for 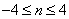
Which is of finite duration
But
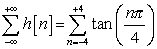
diverges (i.e. it is not absolutely summable) .
Hence the system is unstable.
(e) False
Counter example:
Let
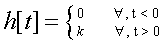
which is causal.
but unstable.
(f) False.
Counter example:
Let 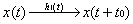
which is non-causal
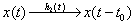
which is causal.
Cascade of the two system
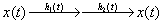
which is clearly causal.
(g) False
Counter example: Let
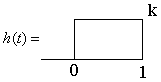
Here
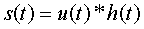
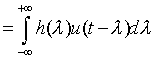
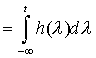
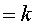
but
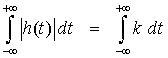
which is divergent.
(h) True
Sufficiency: 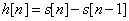
if
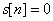 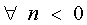
Let n < 0
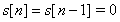
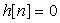 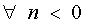
=>causality.
Necessity :
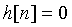 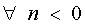
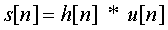
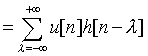
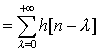
if
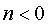 , ,
then
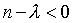 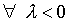
Thus s[n] = 0 for n < 0 . 
|