| |
The linearly independent solutions for 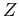 are the Bessel functions of the first kind are the Bessel functions of the first kind 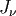 and second kind and second kind 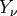 (sometimes denoted by (sometimes denoted by 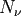 ), where ), where 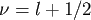 , the order is half integral. Therefore the linearly independent solutions for , the order is half integral. Therefore the linearly independent solutions for 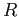 are the spherical Bessel functions, are the spherical Bessel functions, |
|
where the constant factor 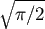 is introduced to comply with standard definitions.
Two linearly independent solutions which can be constructed by taking suitable linear combinations of is introduced to comply with standard definitions.
Two linearly independent solutions which can be constructed by taking suitable linear combinations of 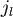 and and 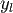 are the spherical Bessel functions of third kind (also known as spherical Hankel functions) : are the spherical Bessel functions of third kind (also known as spherical Hankel functions) : |
|
| which are relevant for scattering problem, as will be seen later. |
|
|
|