| |
| The equations above are not sufficient for a given situation/material and must be supplemented with the so called Constitutive Relations, which are assumed to have the form |
|
where
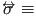 conductivity tensor, conductivity tensor,
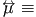 permeability tensor, permeability tensor,
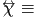 elctric susceptibility tensor, and elctric susceptibility tensor, and
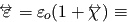 permittivity tensor, which all depend on the material medium. If these are independent of the field, then the medium is said to be linear ; if independent of position (to be more precise, choice of origin for position coordinates), e.g., in a uniform system of infinite extension, the medium is said to be homogeneous ; if independent of direction (e.g., in a uniform system of spherical shape), then the medium is isotropic. permittivity tensor, which all depend on the material medium. If these are independent of the field, then the medium is said to be linear ; if independent of position (to be more precise, choice of origin for position coordinates), e.g., in a uniform system of infinite extension, the medium is said to be homogeneous ; if independent of direction (e.g., in a uniform system of spherical shape), then the medium is isotropic. |
Note that, in general, the symbol `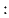 ' for example, in ' for example, in
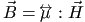 implies the following: implies the following: |
|
and so on. Note that above uses the so called causality condition (i.e., physical effects can only follow the cause, independently of the time origin) which requires that
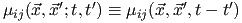 , for , for  , and zero otherwise; for a homogeneous system, one further has , and zero otherwise; for a homogeneous system, one further has
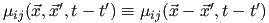 , and for isotropic system, , and for isotropic system,
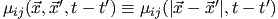 ; similar arguments apply to ; similar arguments apply to
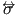 and and
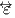 , and will be understood in the following developments. Note also that only for a homogeneous medium, for which , and will be understood in the following developments. Note also that only for a homogeneous medium, for which
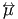 is often approximated to be local (its validity is justified only through detailed response theory), i.e., is often approximated to be local (its validity is justified only through detailed response theory), i.e.,
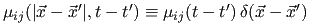 , leads to , leads to |
|
| and similar relations for other fields. |
|
|
|