| |
| The set of four equations |
|
are called Maxwell's equations. The quantity
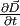 has the dimension of has the dimension of
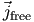 , and Maxwell called it Displacemnt current. These equations form the basis of all classical electromagnetic phenomena. , and Maxwell called it Displacemnt current. These equations form the basis of all classical electromagnetic phenomena. |
The electric displacement field 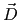 and the magnetic field and the magnetic field 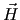 are defined by are defined by |
|
where
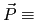 electric polarization = average electric dipole moment per unit volume, electric polarization = average electric dipole moment per unit volume,
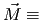 magnetization = average magnetic dipole moment per unit volume, magnetization = average magnetic dipole moment per unit volume,
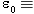 the free space permittivity and the free space permittivity and 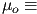 the free space permeability. Note that the free space permeability. Note that 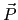 - -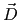 relationship implicitly assumes that relationship implicitly assumes that 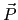 is entirely due to dipole moments, and the contributions from quadrupole and higher moments are negligible. is entirely due to dipole moments, and the contributions from quadrupole and higher moments are negligible. |
|
|
|