| |
Heat Utilization: Concepts
Efficient utilization of fossil fuel reserves requires, in addition to other factors, utilization of heat of POC exiting the furnace. It is well known that potential energy of fuel at 25oC on combustion is converted into the sensible heat pf products of combustion at the flame temperature. Products of combustion after transferring their heat to the furnace chamber exit the furnace. Heat carried by products of combustion depends on the temperature of the furnace; higher is the furnace temperature higher is the amount of heat carried by POC. It may range somewhere in between 40 to 60% of the calorific value of fuel. Heat of POC can be recovered either external to the furnace by installing a heat exchanger or internally by recirculating the POC into the flame in the furnace itself. The former is called external heat recovery and the later is internal heat recovery.
In the following we discuss the principles of external heat recovery of POC. Normally a heat exchanger is integrated with the furnace which captures and reuses the heat of POC simultaneously.
Thermodynamic principles of capture and re-use of heat of POC:
Capture and re-use of heat of POC must be integrated. A heat exchanger integrates capture and reuse of heat. In the heat exchanger hot fluid (POC) flows co-current or counter-current to cold fluid, say air. Both fluids are separated by a wall. Hot fluid enters the heat exchanger at temperature Th1 and exits at temperature Th2 (Th2 < Th1). Wall is heated by the heat transferred from the hot POC. Cold fluid enters the heat exchanger at temperature Tc1 and leaves at Tc2 such that Tc2> Tc1.
Heat balance over an infinitesimally small element of length dx can be written at steady state
Heat lost by hot fluid = Heat gained by the cold fluid − Heat loss from the element to the surrounding
Let mh, and mc are mass of hot fluid and cold fluid, CPh and CPc are the specific heat of hot and cold fluid then we can write
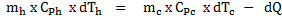 5) 5)
In eq. 2 dTh and dTc are the change in temperatures of hot and cold fluid at any position along the length of the exchanger.
In an ideal adiabatic-reversible heat exchange between hot and cold fluid, dQ = zero and the process is reversible when temperature difference between hot and cold fluid at any position along the length of the heat exchanger, i.e.∆Ti = (dThi − dTci) = o provided
mh x CPh = mc x CPc.
This is possible when both fluids have infinite contact time, and separating wall has zero thermal resistance. In this situation the temperature difference between hot and cold fluid at any position will be very small and constant along the length of the heat exchanger.
Finite thermal resistance of the separating wall and flow rates of both fluids make the heat exchange irreversible. Finite flow rates of both fluids will have finite residence time depending on flow rates and as a result all the heat is not transferred from hot to cold fluid. Similarly finite thermal resistance of the wall will also limit the transfer of heat to the cold fluid. In such a situation for an adiabatic process .
∆Ti = (dThi − dTci) will be non-zero, but will have constant value when mh x CPh = mc x CPc .
The practical result of the irreversibility is that the heat exchange is not complete and there is always some heat which is left with the POC on leaving the heat exchanger.
Difference in heat capacities of fluid will influence the heat exchange process. For example if CPh> CPc, cold fluid can be heated nearly to the entering temperature of hot fluid provided mh = mc.
|