| |
According to equation 1 heat loss to the surrounding depends on the inside surface temperature of the refractory, furnace and surrounding temperatures and the thermal resistance offered by the refractory wall. Consider a 0.23m firebrick wall of thermal conductivity 1.731 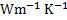 at 1273K inner surface temperature of the refractory. Heat loss per unit area from this wall to the surrounding is calculated to be at 1273K inner surface temperature of the refractory. Heat loss per unit area from this wall to the surrounding is calculated to be 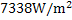 for the surrounding temperature of 298K. Assuming reflectively of the refractory for the surrounding temperature of 298K. Assuming reflectively of the refractory 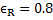 and heat loss as and heat loss as 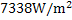 , furnace temperature can be calculated to be 1292K which is only , furnace temperature can be calculated to be 1292K which is only 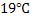 higher than the inner surface temperature of the refractory. The difference between the inner surface temperature of the refractory and the furnace temperature can be reduced further by increasing the thickness of the wall and using refractory of lower thermal conductivity. This calculation suggests that the inner surface temperature of the refractory wall is close to the average temperature of the furnace. higher than the inner surface temperature of the refractory. The difference between the inner surface temperature of the refractory and the furnace temperature can be reduced further by increasing the thickness of the wall and using refractory of lower thermal conductivity. This calculation suggests that the inner surface temperature of the refractory wall is close to the average temperature of the furnace.
The role of refractory surface can be illustrated. For the firebrick wall the total incident flux is . 157991W/m2 at furnace temperature 1292K.Of this incident flux, 30130W/m2 is reflected back into the furnace and 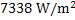 is lost to the surrounding through the wall of the refractory. The balance 120523W/m2 is absorbed and re-readiated by the refractory back into the furnace. Thus refractory surface is an efficient reflector (76%) but the mechanism of reflection is absorption and re-radiation. is lost to the surrounding through the wall of the refractory. The balance 120523W/m2 is absorbed and re-readiated by the refractory back into the furnace. Thus refractory surface is an efficient reflector (76%) but the mechanism of reflection is absorption and re-radiation.
|