The expression 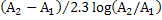 is known as logarithmic mean area. Consider a thin walled pipe or a duct with a wall thickness less than inside diameter is known as logarithmic mean area. Consider a thin walled pipe or a duct with a wall thickness less than inside diameter 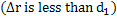 , the area ratio , the area ratio 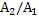 is less than 2 and the logarithmic mean area is substantially equal to the arithmetic mean area is less than 2 and the logarithmic mean area is substantially equal to the arithmetic mean area 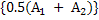 . However, if . However, if 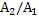 is greater than 2 which could be a thick-walled pipe or thick insulation of small pipes or tube furnaces, use of arithmetic mean area would predict higher heat losses than the logarithmic mean area. is greater than 2 which could be a thick-walled pipe or thick insulation of small pipes or tube furnaces, use of arithmetic mean area would predict higher heat losses than the logarithmic mean area.
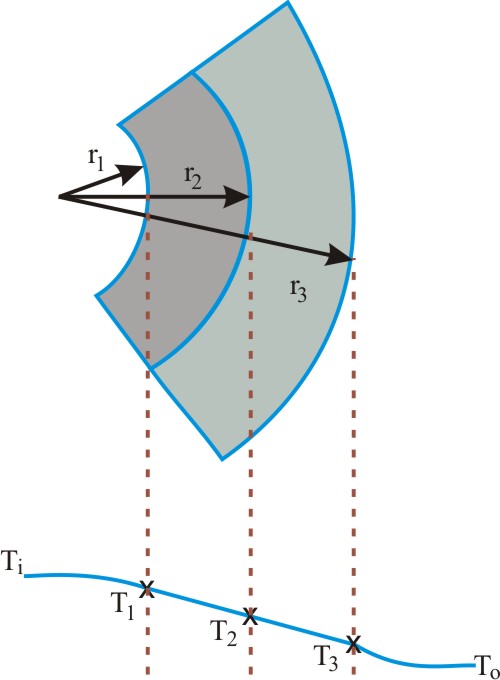
Figure 4 is the construction of a composite cylindrical wall having radius 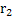 and and 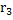 measured from the centre of the cylinder of radius measured from the centre of the cylinder of radius 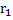 such that such that 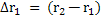 and and 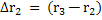 . The thermal conductivity of the refractory material of thicknesses . The thermal conductivity of the refractory material of thicknesses 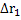 and and 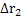 is is 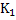 and and 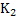 respectively. The length of the cylinder is respectively. The length of the cylinder is  . As in the case of flat wall . As in the case of flat wall 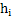 and and 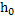 are the heat transfer coefficients that determine surface temperatures are the heat transfer coefficients that determine surface temperatures 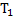 and and 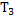 . The composite wall is placed in between furnace temperature . The composite wall is placed in between furnace temperature 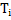 and environment temperature and environment temperature 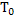 . .
 |
| Figure 29.4: |
Temperature distribution in a composite cylindrical wall of different diameters at steady state. |
As no heat is produced in the composite wall, steady state heat flow for the length of the cylinder  is is
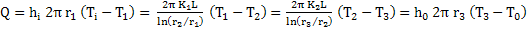 |
(9) |
Adding thermal resistance in series
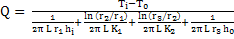 |
(10) |
The equation 10 determines the heat flow in a composite wall. The temperature profile is as shown in the figure by the solid line.
|