| |
6.10.2 Frequency Response of Permeability
It is given that ferro- and ferri-magnetic materials have permanent moments which constitute regions of aligned moment called as domains with two regions of different regions separated by a domain wall. Now, the ease of domain wall movement can be described in terms of coercivity, i.e. the higher the coercive field, the easier it is for domains walls to move during switching.
So, all we can say at this point is that this domain wall movement is dependent on the frequency of the applied field. In some materials, low frequencies are needed for easy switching while some materials can witness easy switching at GHz or microwave region frequencies making them suitable for microwave devices.
This also means that permeability, μ, in a similar manner as permittivity in dielectrics, can be defined as a complex quantity i.e. μ* = μ' + μ'' where μ' is the real part of permeability and μ'' is the complex part of the permeability.
6.10.2.1 Proof:
While at low frequencies in a linear magnetic material, B = μ0µrH, at high frequencies, these two parameters are related to each other with some lag time. These fields can be written as phasors, such that
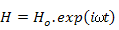 and and 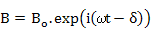 |
|
where δ can be expressed as the phase delay of B from H.
Now, we can define the magnetic permeability as
The above equation clearly states that magnetic permeability is a complex quantity.
We can further simplify equation (6.39) into
Hence, the loss tangent is defined as the ratio of the imaginary to the real part of the complex permeability and is
Loss tangent is representative of how much power is lost in a material versus how much is stored. |