| |
1.7.2 Antifluorite (A2X) and Fluorite (AX2) Structures
1.7.2.1 Antifluorite
FCC packing of anions All tetrahedral sites filled by cations Coordination : Anions: 8, Cations: 4 Chemical formula: M2X -
Example: Li2O, Na2O, K2O
Radius ratio (rc/ra): 0.225-0.414 Examples: r(Li+)
:
0.059 nm,
r(Na+)
:
0.099 nm,
r(O-)
:
0.14 nm
| Figure 1.25 Antifluorite structure |
Lattice type: FCC Motif – X: 0 0 0, M - 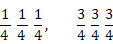
Four formula units per unit cell -
In this structure in many cases, although rc/ra ratio predict an octahedral co-ordination, tetrahedral coordination is preferred to fulfill the stoichiometry requirements. In turn, anions are cubic coordinated by cations (CN: 8)
The structure shows corner sharing of tetrahedra.
1.7.2.2 Fluorite Structure (CaF2 Structure)
Slightly bigger cations in comparison to other structures -
Example:UO2, ZrO2, CaF2, CeO2
Typical representation of the structure appears as if cations make a FCC lattice and anions occupy the tetrahedral sites.
| Figure 1.26 Fluorite Structure |
While more appropriate Fluorite structure representation is shown below where eight primitive cubic unit cells made by anions are joined together to make a big cube and cations occupy the centers of four of these small cubes in an ordered fashion.
| Figure 1.27 A more appropriate representation of fluorite structure |
Co-ordination number: Cations - 8 ; Anions - 4 -
Lattice: FCC
Motif: M – 0 0 0; X – ¼ ¼ ¼; ¾ ¾ ¾ Examples of ionic radii of a few ions: U4+ : 0.1 nm, Zr4+: 0.084 nm, Ce4+: 0.097 nm, O2- : 0.14 nm (observe that cations are quite large as compared to oxygen ions) The structure as you can also see has a large void in the center of unit cell made by cations. These empty spaces make such oxides, good ionic conductors which is useful in applications such as energy storage e.g. batteries. For having some fun with the structure, we can also draw as projection of this material on (110) plane. Here you can see the row of empty octahedral sites along [110]-direction.
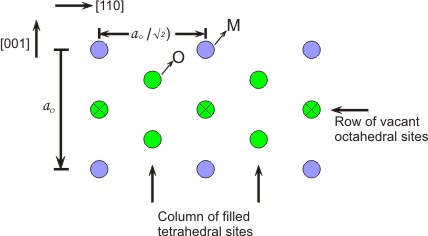 |
| Figure 1.28 View of (110) plane of fluorite structure |
|