4.4 Determination of Local Field
The local field, Eloc, experienced by an atom or dipole or molecule usually differs from the applied field, Eex owing to the polarization of the surrounding medium around a dipole or molecule.
While on a macroscopic scale, the overall field in a material is zero due to the condition of electrical neutrality, when we start looking at the scale of individual atoms and molecules, it is not the case. Although this local field which is nothing but the sum of applied field and some other fields and can, in principle, be solved using Poison’s equation, coupling charge density and potential at each location, the method is far from being simple. Instead, we use a simple approach, by using Lorentz model where we divide the field into different components.
The understanding of this field can be obtained from the figure shown below which shows a sphere of dielectric material, say containing about 10 atoms, removed. The local field at the center of this sphere is composed of two macroscopic fields and two microscopic fields.
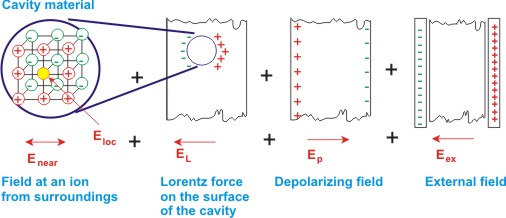 |
| Figure 4.8 Schematic representation of various electric fields when a small cavity is created in a dielectric |
The microscopic fields are:
Ecenter, field at the center of the sphere due to contributions of ions surrounding it with-in the sphere. EL, Lorentz field at the center of the spherical cavity due to charges on the surface of the cavity
(Note the difference between the two: one is talking of a sphere while it is composed of material and another is talking of a material surrounding the spherical cavity from which material has been removed.)
The macroscopic fields considering the dielectric as a continuum are:
Eex, field due to applied voltage across the capacitor Ed, the depolarizing field due to dielectric polarization
Hence, Eloc is written as
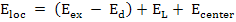 |
(4.22) |
Now, we know that
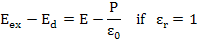 |
(4.23) |
Lorentz showed that for isotropic crystals,Ecenter= 0
EL can be worked out for a cavity as
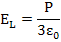 |
(4.24) |
(Analysis of the Lorentz field in the next slide)
Hence the local field is given as
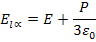 |
(4.25) |
By substituting P = ε0 (εr - 1)E in (4.25)
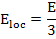 ( (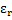 + 2) + 2) |
(4.26) |
Now combining equations (4.20) and (4.26), we get
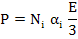 ( (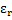 + 2) + 2) |
(4.27) |
Combining (4.15) and (4.27), we get
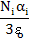 = = 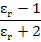 |
(4.28) |
The above equation is called Clausius-Mossotti relationship and is valid only for linear dielectrics. The equation is related to a macroscopic quantity on RHS, i.e. εr with a microscopic quantity, α.
As a result, if one knows the dielectric constant by means to measurement, this form can be used to calculate the polarizabilities of a variety of materials to quite an accurate estimate.
Polarizability, α, is the sum of polarizabilities from all the contributing mechanisms i.e. αelectronic, αionic, αdipolar and αinterfacial.
Special case:
For gases
And hence at low pressures
Thus
|