4.2 Mechanisms of Polarization

Basically, there are four mechanisms of polarization:

• Electronic or Atomic Polarization

This involves the separation of the centre of the electron cloud around an atom with respect to the centre of its nucleus under the application of electric field (see (a) in figure below).

• Ionic Polarization

This happens in solids with ionic bonding which automatically have dipoles but which get cancelled due to symmetry of the crystals. Here, external field leads to small displacement of ions from their equilibrium positions and hence inducing a net dipole moment (see (b)).

• Dipolar or Orientation Polarization

This is primarily due to orientation of molecular dipoles in the direction of applied field which would otherwise be randomly distributed due to thermal randomization (see (c and d)) and finally

• Interface or Space Charge Polarization

This involves limited movement of charges resulting in alignment of charge dipoles under applied field. This usually happens at the grain boundaries or any other interface such as electrode-material interface (see (e and f))

.

Figure 4.6 Schematic of mechanisms of polarization

Atomic polarization is present in all materials by definition and hence any other mechanism would be an addition.

While mathematical treatment of the first three mechanisms is rather straightforward, interface polarization is not easy to quantify.

Qualitatively, we can see that in the above four mechanisms, the masses of the entities to be displaced are different, with mass getting larger from electronic to ionic to dipolar polarization. This has a direct relation with the frequency of the applied field (see figure below). Intuitively, we can mention that heavier the particular entity, more is the time spent in displacing it. As a result, atomic polarization is the fastest and typically persists at frequencies between ~10¹³-10¹⁵ Hz. In contrast, ionic polarization is sluggish and typically occurs at frequencies between ~10⁹-10¹³ Hz while dipolar polarization involving movement of molecules happens below 10⁹ Hz. Interface or space charge polarization occurs at frequencies below 10 Hz.

For non-magnetic dielectrics, Maxwell’s electromagnetic theory predicts that the dielectric constant obtained from the electronic contribution is also related to the index of refraction as ε_{r =} n² which is true at very high frequencies, above 10¹²-10¹³ Hz. Contribution from any other mechanism will be on top of it. So the total dielectric constant for a material would be ε_r-electronic (= n²) + e_r-ionic + ε_r-dipolar.

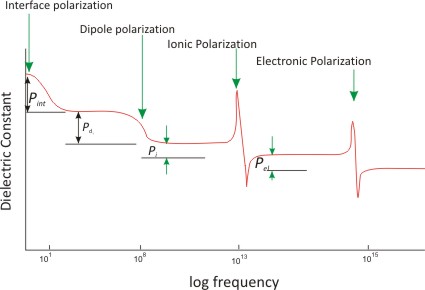Figure 4.7 Schematic figures between dielectric constant vs frequency showing various mechanisms

The following table shows the values of ε_r and n² for a variety of materials and the dominant polarization processes in them:

Material	εr	n2	Dominant mechanisms
C (Diamond)	~5.7	5.85	Electronic
Ge	~16	16.73	Electronic
NaCl	~5.9	2.37	Electronic and Ionic
Water (H2O)	~80	1.77	Electronic, Ionic and Dipolar


So, you can see that while carbon and germanium being single elemental materials show electronic polarization only and as a result their dielectric constants match well with the values of n². However, the same is not the case with NaCl or water which have strong contributions of ionic and ionic and dipolar polarization respectively. We will discuss more about these processes in the latter sections.