3.15 Nernst Equation and Application of Ionic Conductors
We have seen that the electrochemical potential is a combination of chemical potential and electrical potential.
Applied chemical potential gradient gives rise to a voltage which is useful in the operation of devices like batteries, fuel cells, sensors.
Ionic transport is essential for the imposed oxygen pressure gradient to establish a gradient in the oxygen concentration. Simultaneously, electronic conduction must be avoided to prevent short circuiting which requires ti ≈ 1.
Consider two sides separated by an electrolyte. At equilibrium, the chemical potential of both the sides is equal, i.e.
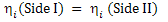 |
(3.58)
|
Electrical potential across the electrolyte is related to the chemical potential difference by

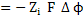
|
(3.59)
|
Chemical potential can be expressed as
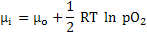 |
(3.60) |
Thus,
The above equation is referred to as Nernst Equation.
For partially ionic conduction, equation (3.61) can be modified to
|