Conduction in ionic solids is not similar to the band transport in metals and semicoductors. Conduction in these solids is often governed by concentration of impurities, dopants and point defects.
Conduction in these materials tends to be of polaronic or hopping type which is migration of charges between either two dissimilarly charged ions or counter migration of ions and defects such as vacancies.
In ionic solids, proximity of the carriers to the ions results in the formation of a polarized region i.e., a polaron which may be longer or smaller than size of the unit-cell.
-
Effective mass, m* , depends on level of interactions between electrons or holes and periodic lattice potential.
-
Effective mass can be taken as equal to that of a free electron i.e. me* = mfree electron*. Large polarons typically depict weak interaction between carries and ions and hence electronic mobility expressions can be valid for the polaron.
-
In a number of of ionic systems such as LiNbO3, COFe2O4, FeO etc., carrier-ion interaction is strong and these are called as strongly-correlated-systems, In such cases, polarons are of smaller sizes and the effective mass tends to be larger than that of a free electron.
In such systems, motion of carriers is thermally activated i.e. via hopping mechanism.
-
For example, Li2O doping in NiO under oxidizing conditions gives rise to oxidation of Ni2+ ions to Ni3+ ions (write the defect reaction yourself). Mixed presence of Ni ions in +2 and +3 states leads to hopping type conduction of electrons between two states. This conductivity of NiO increases as Li doping is increased as shown schematically in Figure 3.4.
Ni3+ acts as a perturbing charge which polarizes the lattice surrounding it leading the formation of Polaron.
| Figure 3.4 Example of change in resistivity (ρ) of NiO upon doping with Li2O |
The movement of carrier between these differently charged states can happen by hopping which is a thermally activated phenomenon.
Conduction in such cases is determined by dopant concentration and hence higher the dopant concentration (within appropriate limits), higher the conductivity. In contrast, in the band model, carrier concentration is determined by temperature.
In ionic solids, while carrier concentration is independent of temperature (within extrinsic region), mobility is strongly affected by temperature as is also obvious from equation (3.33) and is expressed as
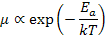 |
(3.38) |
where Ea is the activation or migration energy.
Typically carrier mobilities in strongly interacting ionic systems are of the order of ~0.1 cm2/V-s which are about 3-4 orders of magnitude smaller as compared to the weakly interacting systems where carrier mobilities can be between 100-1000 cm2/V-s.
Table 3.1 lists some of the mobility values in oxides and for comparison, other materials are listed too.
Table 3.1: Approximate Carrier Mobilities at Room Temperature
Mobility ( cm2 /V sec) |
Mobility ( cm2/V sec) |
Crystal |
Electrons |
Holes |
Crystal |
Electrons |
Holes |
Diamond |
1800 |
1200 |
PbS |
600 |
200 |
Si |
1600 |
400 |
PbSe |
900 |
700 |
Ge |
3800 |
1800 |
PbTe |
1700 |
930 |
InSb |
105 |
1700 |
AgCl |
50 |
|
InAs |
23,000 |
200 |
KBr ( 100 K ) |
100 |
|
InP |
3400 |
650 |
CdTe |
600 |
|
GaP |
150 |
120 |
GaAs |
8000 |
3000 |
AlN |
-- |
10 |
SnO2 |
160 |
|
|
-- |
~0.1 |
SrTiO3
Fe2O3
TiO2
Fe3O4 |
6
0.1
0.2
… |
0.1 |
GaSb |
2500-4000 |
650 |
CoFe2O4 |
10-4 |
10-8 |