| |
3.2 Diffusion Kinetics
Typically diffusion is explained on the basis of compositional gradients in an alloy which act as driving force for diffusion. Thermodynamically speaking, this amounts to gradient in the chemical potential which drives the migration of species from regions of higher chemical potential to lower chemical potential so that system reaches a chemical equilibrium. The atomic flux as a result of driving force is expressed in terms of chemical composition gradient, also called as Fick’s law(s). These laws are briefly explained below. For detailed discussion on diffusion, readers are referred to standard text books on diffusion.1,2
3.2.1 Fick's First Law of Diffusion
It states that atomic flux, under steady-state conditions, is proportional to the concentration gradient. It can be stated as
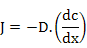 |
(3.1) |
where
-
J is the diffusion flux with units moles/cm2-s, and basically means the amount of material passing through a unit area per unit time;
D is the proportionality constant, called as diffusion coefficient or diffusivity in cm2/s;
x is the position in cm; and
-
c is the concentration in cm3 .
The negative sign on the R.H.S. indicates that diffusion takes place from regions of higher concentration to lower concentration i.e. down the concentration gradient. Diffusivity is a temperature dependent parameter and is expressed as D = D0 exp (-Q/kT) where Q is the activation energy, k is Boltzmann's constant and D0 is the pre-exponential factor in cm2 /s.
3.2.2 Fick's Second Law of Diffusion :
Strictly speaking it is not a law, but rather a derivation of the first law itself. It predicts how the concentration changes as a function of time under non-steady state conditions . It can be derived from Fick's first law easily. For further discussions, one can refer to “Diffusion in Solids”, a classic book written by Paul Shewmon and published by Wiley or other NPTEL courses related to Phase Transformations and Diffusion.
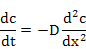 |
(3.2) |
where t is the time in seconds. Other terms are defined above.
1Diffusion in Solids, Paul Shewmon, Wiley
2Diffusion in Solids, Martin Glicksman, Wiley-Interscience |
|