Formulation of mechanical impedance for a composite laminate
In Lecture 22, the equation of motion of a general dynamical system has been presented [Equation 22.3] as
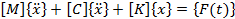 |
(27.1) |
The equation may be transformed into state-space form as
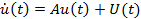 |
(27.2) |
by introducing 2n- dimensional state vector, q(t) and excitation vector, Q(t), followed by Cholesky decomposition and linear transformation.
Here 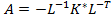 is a real nonsymmetrical matrix and is a real nonsymmetrical matrix and 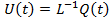 is a real vector. is a real vector.
The solution of the above equation may be obtained by modal analysis which amounts to the determination of the Jordan form for A.
The eigen value problem associated with Equation (27.2) has the solution of the form
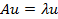 |
(27.3) |
The solution consists of 2n eigen values 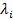 and 2n eigen vectors and 2n eigen vectors 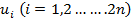 . .
The Jordan matrix is diagonal and may be expressed as
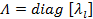 |
(27.4) |
Eigen vectors 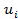 , known as right eigen vectors of A, can be arranged in the square matrix , known as right eigen vectors of A, can be arranged in the square matrix
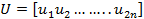 |
(27.5) |
Similarly, left eigen vectors could be arranged in a square matrix as
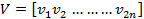 |
(27.6) |
The set of eigen vectors 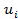 is orthogonal to the set of eigen vectors is orthogonal to the set of eigen vectors 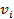 and the eigen vectors may be normalized so as to satisfy and the eigen vectors may be normalized so as to satisfy
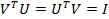 |
(27.7) |
in that case, the Jordan matrix is simply represented as
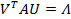 |
(27.8) |
Either set of eigen vectors can be taken as a basis for 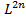 . .
Assuming that the solution of equation has the form
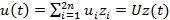 |
(27.9) |
where 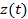 is a 2n vector with components is a 2n vector with components 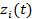 . .
|