Response of a General Dynamic System
The equation of motion for a general dynamical system is in the form
The matrix C is arbitrary and may not be symmetric. The system must be treated as a general one. It is assumed that M and K are positive definite.
Introducing the 2n- dimensional state vector 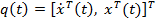 and the 2n-dimensional excitation vector, and the 2n-dimensional excitation vector, 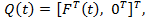 Equation (22.2) can be transformed into Equation (22.2) can be transformed into
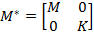 and and 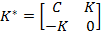 are real are real 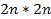 matrices. matrices. 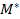 is a positive definite symmetric matrix. is a positive definite symmetric matrix. 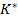 is neither positive definite nor symmetric. is neither positive definite nor symmetric.
Equation (22.4) can be rendered into a more convenient form by the Cholesky decomposition
Then, introducing the linear transformation
where 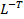 = ( = (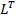 ) = ) = 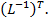
Equation (22.5) can be reduced to
in which 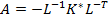 is a real non symmetrical matrix and is a real non symmetrical matrix and 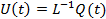 is a real vector. is a real vector.
Since this is a free vibration case, 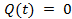 , Hence, Equation (22.7) reduces to , Hence, Equation (22.7) reduces to
The solution of Equation (22.8) may be expressed as
The final response may be obtained from Equation (22.9)
|