A quintic polynomial series is adopted for the transverse displacement function
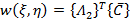 |
(18.11) |
where,
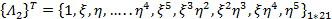 |
(18.12) |
By using Equation (18.7), each elements of U can be expressed in terms of the elements of C. There are ten such relations corresponding to the ten in-plane DOF which can be summarized as a matrix equation.
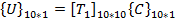 |
(18.13) |
The constants of the in-plane displacement polynomial can be expressed in terms of U as
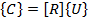 |
(18.14) |
where
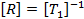 |
(18.15) |
However, using this relation, the in-plane displacement field u can be expressed in terms of nodal DOF U as
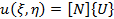 |
(18.16) |
Similarly,
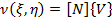 |
(18.17) |
and
 |
(18.18) |
where,
 and and 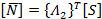 |
(18.19) |
 and and  are the transformation matrices between natural and global coordinates. are the transformation matrices between natural and global coordinates.
|