|
Exercise Problems - Chapter 9
1.Two students are asked to solve the Blasius flow over a flat plate to determine the variation of boundary layer thickness as a function of the Reynolds number. One student solves the problem by similarity method and arrives at the result 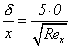 .
The other student chooses to solve the problem by using the momentum-integer equation and Karman-Pohlhausen method and funds that .
The other student chooses to solve the problem by using the momentum-integer equation and Karman-Pohlhausen method and funds that 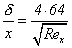 . .
Which of the two results is expected to be closer to the experimental results and why?
2. A scientist claims that a highly viscous flow around a body can generate the same flow patterns as the flow of an inviscid and incompressible fluid around that body. According to our understanding, the Reynolds number for the first flow is very small, while the Reynolds number for the second flow can be taken to be 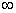 (infinity). Do you think it is possible to get the same flow patterns for the two extreme values of Reynolds number? Please use mathematical analysis to prove or disprove the scientist's claim. (infinity). Do you think it is possible to get the same flow patterns for the two extreme values of Reynolds number? Please use mathematical analysis to prove or disprove the scientist's claim.
3. In boundary layer theory, a boundary layer can be characterized by any of the following quantities (i) Boundary layer thickness (ii) Displacement thickness (iii) Momentum thickness.
How do these quantities differ in their physical as well as mathematical definitions? For the flow over a flat plate, which of these is expected to have the highest value at a given location on the wall, and which the lowest?
4.
What do you mean by the "point of separation" of a boundary layer? How will the velocity gradient 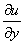 and the second gradient and the second gradient 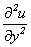 .Vary within the boundary layer at the point of separation? Please show the variation graphically. Here u is the velocity along the wall and y is the co-ordinate perpendicular to the wall. .Vary within the boundary layer at the point of separation? Please show the variation graphically. Here u is the velocity along the wall and y is the co-ordinate perpendicular to the wall.
5. Reduce the Prandtl's boundary layer equations to a simpler form than that given by equations (28.10) - (28.12) for -
(a) Flow over a flat plate.
(b) The case
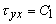 (a constant) (a constant)
(c) The case where velocity (v) is directly proportional to kinematic viscosity (
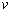 ) )
(d) Also solve the Prandtl's boundary layer equations for v =
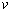 assuming pressure gradient assuming pressure gradient 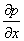 =0. =0.
6. Water of kinematic viscosity (
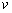 ) equal to 9.29x10 -7 m2 /s is flowing steadily over a smooth flat plate at zero angle of incidence, with a velocity of 1.524 m/s. The length of the plate is 0.3048 m. Calculate- ) equal to 9.29x10 -7 m2 /s is flowing steadily over a smooth flat plate at zero angle of incidence, with a velocity of 1.524 m/s. The length of the plate is 0.3048 m. Calculate-
(a) The thickness of the boundary layer at 0.1524 m from the leading edge.
(b) Boundary layer rate of growth at 0.1524 m from the leading edge.
(c) Total drag coefficient on the plate.
7. Use the Prandtl's boundary layer equations and show that the velocity profile for a laminar flow past a flat plate has an infinite radius of curvature on the surface of the plate.
8. Air is flowing over a smooth flat plate at a velocity of 4.39 m/s. The density of air is 1.031 Kg/m3 and the kinematic viscosity is 1.34x10-5 m2 /s. The length of the plate is 12.2 m in the direction of the flow. Find-
(a) The boundary layer thickness at 15.24 cm from the leading edge.
(b) The drag coefficient (CDf ).
9. Show that the shape factor (H) has the value 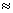 2.6 for the boundary layer flow over a flat plate. Also calculate the position where the flow is critical for flow velocity of 3.048 m/s and kinematic viscosity 9.29x10 -7 m2 /s. 2.6 for the boundary layer flow over a flat plate. Also calculate the position where the flow is critical for flow velocity of 3.048 m/s and kinematic viscosity 9.29x10 -7 m2 /s.
Given that at the critical location Reynold's Number (based on distance from the leading edge surface) is related to shape factor (H) by-
log(R critical ) =H.
10. Determine the distance downstream from the bow of a ship moving at 3.9 m/s relative to still water at which the boundary layer will become turbulent. Also find the boundary layer thickness and total friction drag coefficient for this portion of the surface of the ship. Given the kinematic viscosity = 1.124x10-6 m2 /s.
To
view the recap, click next button or select from left-hand-side. |
|