Exercise Problems  -  Chapter 5

1.  An open cylindrical tank 2m high and 1 m in diameter, is filled with water to a depth of 1m. If the cylinder rotates about its vertical axis. Determine

                          (a)       the maximum angular velocity of the cylinder without spilling any water
                          (b)       the depth at the center and gauge pressure at the bottom 0·2 m from the center at the condition of maximum angular velocity

(6.26 rad/s, zero, 783.75 Pa.)

2.  The velocity distribution for laminar flow between two parallel plates is given by

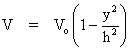
where 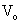is the center plane velocity, h is the half spacing between the plates and y is the normal distance from the center plane. Determine the

            (a)    average velocity
            (b)    momentum correction factor

3.  Flow of air at 50°C is measured by a pilot-static tube. The differential reading in a water manometer is 24 mm. Determine the velocity of air if the coefficient of tube is 0·95. Assume the density of air to be constant at 1·2 kg/m³

(6 m/s)

4.  Consider a short cylindrical duct whose cross-section enlarges abruptly from a diameter D₁ to a diameter D₂ . Find the ratio D₁ /D₂ so that the pressure drop for a given flow rate of a fluid through the duct is independent of the direction of flow. Neglect the losses due to skin friction. (Take co efficient of contraction C_c = 0.6)

(0.577)

5.  A venturimeter is placed at 30° to the horizontal ( sloping upwards in the direction of flow) to a pipe line carrying an oil of specific gravity 0·8. A differential manometer with mercury as the manometric fluid is attached to the inlet and throat of the venturimeter. The manometer shows a deflection ( the difference in height between the menisci of mercury at the two limbs) of 100mm. The pipe diameter is 200 mm, while the diameter of venturi throat is 100 mm.

            (a)     Find the volume flow rate of oil if the coefficient of discharge of the venturimeter is 0·96.
            (b)     What will be the reading of differential manometer if the venturimeter is turned horizontal? The length of venturimeter between the inlet and the throat is 320 mm.

(0.044 m³ /s, 110 mm)

6. Fig. 16.6 shows the weight W supported by the pressure difference created in the venturi and applied across the piston. At the inlet the air velocity is 10 m/s and the area is 100 cm². The throat area is 4 cm². Given that the air density is equal to 1.2 kg/m³, calculate the weight W that will be in equilibrium. Assume ideal flow in the duct, no friction between the piston and cylinder, and the piston has no mass.

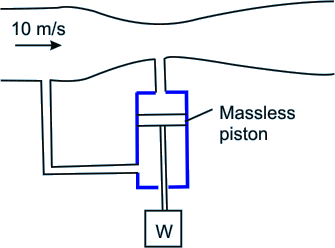
Figure 16.6

(18.72 N)

7. A fire-fighting hose with an exit nozzle diameter = 50 mm discharges water at the rate of 3000 litres per minute. The height of the nozzle exit from the pump is 4 m and water level in the sump is 1 m below the pump (see Fig. 16.7 ). Calculate the head and power developed by the pump. Assume there are no losses in the pipeline and pump.

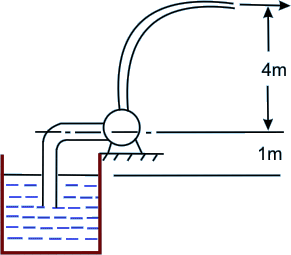
Figure 16.7

(38.17 m, 18.72 kw)

8. A free jet of water is produced using a 75 mm diameter nozzle attached to a 200 mm diameter pipe, as shown in Figure 16.8. If the average velocity of water at plane B is 3.8 m/s, calculate the velocity of water at point A in the free jet. Neglect friction losses in the nozzle and pipe.

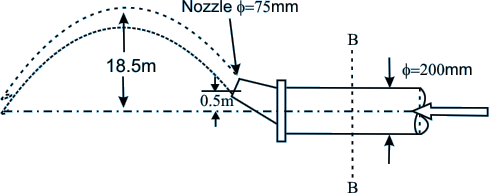
(19.4 m/s)

Figure 16.8