Problem1: 

A velocity field is given by

      a) Find the equation of the streamline at t =t₀ passing through the point (x₀,y₀).

      b) Obtain the path line of a fluid element which comes to (x₀, y₀) at t=t₀.

      c) Show that, if A=0 and B=0 (i.e. steady flow), the streamline and path line coincide.

Solution:

a)      Streamline: Here U_x=(1+At +Bt­­²) and U_y=x.

 Since the slope of the streamline (dy/dx) is the same as the slope (U_y/U_x) of the velocity vector.

Therefore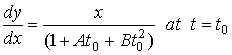     

 Integrating this with the condition x=x₀, y=y₀ gives the Streamline

 b)      Path line: Consider a fluid element passing through (x₀, y₀) at t=t_0. Its co-ordinates (x,y) at other values of t (which define the pathline) can

                be expressed as

          Since,     

And,              

Integrating  the first equation gives,

Now,    

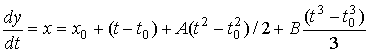
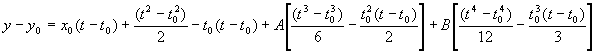
                  These equations of x, y are parametric equation of path line.

                  The time t can be eliminated between them to give an equation for y in terms of x.

        c)    When A=B=0, then the equation of streamline becomes

and the parametric equations of the path line becomes;

Therefore,      

which is equivalent to streamline.

Problem2:

A two-dimensional flow field is defined as

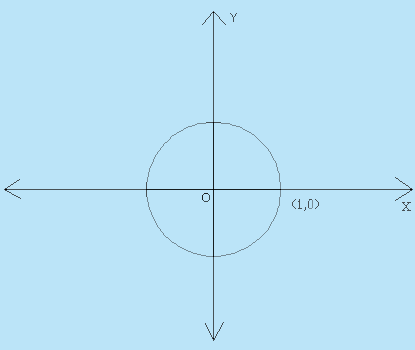
Define the equation of Streamline passing through the point (1,0)

Solution:

The equation of Streamline is

or,  

Hence,   

or,

Integration of equation above gives

where k is constant

For stream line passing through (1,0) ,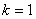

Hence, the required equation is: