|
Streak Lines
Definition: A streak line is the locus of the temporary locations of all particles that have passed though a fixed point in the flow field at
any
instant of time.
Features of a Streak Line:
-
While a path line refers to the identity of a fluid particle, a streak line is
specified by a fixed point in the flow field.
-
It is of particular interest in experimental flow visualization.
-
Example:
If dye is injected into a liquid at a fixed point in the flow field, then at a later time t, the dye will indicate the end points of the path lines of particles which have passed through the injection point.
-
The equation of a streak line at time t can be derived by the Lagrangian method.
If a fluid particle
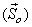 passes through a fixed point passes through a fixed point
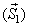 in course of time t, then the Lagrangian method of description gives the equation in course of time t, then the Lagrangian method of description gives the equation
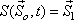 |
(7.5) |
Solving for 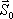 , ,
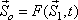 |
(7.6) |
If the positions
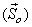 of the particles which have passed through the fixed point of the particles which have passed through the fixed point
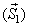 are determined, then
a streak line can be drawn through these points. are determined, then
a streak line can be drawn through these points.
Equation: The equation of the streak line at a time t is given by
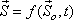 |
(7.7) |
Substituting Eq. (7.5) into Eq. (7.6) we get the final form of equation
of the streak line,
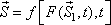 |
(7.8) |
|