|
Description of Fluid Motion
A. Lagrangian Method
-
Using Lagrangian method, the fluid motion is described by tracing the kinematic behaviour of each particle constituting the flow.
-
Identities
of the particles are made by specifying their initial
position (spatial location) at a given time. The
position of a particle at any other instant of time then becomes a function of its identity and time.
Analytical expression of the last statement :
 |
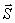 is the position vector of a particle (with respect to a fixed point of reference) at a time t.
 is its initial position at a given time t =t0 |
(6.1) |
Equation (6.1) can be written into scalar components with respect to a
rectangular cartesian frame of coordinates as:
|
x = x(x0,y0,z0,t) |
| (where, x0,y0,z0 are the initial coordinates and x, y, z are the coordinates at a time t of the particle.) |
|
(6.1a) |
|
y = y(x0,y0,z0,t) |
(6.1b) |
|
z = z(x0,y0,z0,t) |
(6.1c) |
Hence 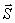in can be expressed as
|
|
 ,  , and  are the unit vectors along x, y and z axes respectively. |
velocity and acceleration
The velocity 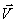 and
acceleration  of the fluid particle can be obtained from the material derivatives of the position of the particle with respect to time. Therefore,
 |
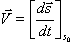(6.2a) |
In terms of scalar components,
where u, v, w are the components of velocity in x, y, z directions respectively.
Similarly, for the
acceleration,
 |
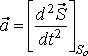(6.3a) |
and hence,
where
ax, ay, az are accelerations in x, y, z directions respectively.
Advantages of Lagrangian Method:
- Since motion and trajectory of each fluid particle is known,
its history can be traced.
- Since particles are identified at the start and traced throughout their motion, conservation of mass is inherent.
Disadvantages of Lagrangian Method:
- The solution of the equations presents appreciable mathematical difficulties except certain special cases and therefore, the method is rarely suitable for practical applications.
|
