Hydrostatic Thrusts on Submerged Curved Surfaces

On a curved surface, the direction of the normal changes from point to point, and hence the pressure forces on individual elemental surfaces differ in their directions. Therefore, a scalar summation of them cannot be made. Instead, the resultant thrusts in certain directions are to be determined and these forces may then be combined vectorially. An arbitrary submerged curved surface is shown in Fig. 5.3. A rectangular Cartesian coordinate system is introduced whose xy plane coincides with the free surface of the liquid and z-axis is directed downward below the x - y plane.

Fig 5.3   Hydrostatic thrust on a Submerged Curved Surface

Consider an elemental area dA at a depth z from the surface of the liquid. The hydrostatic force on the elemental area dA is

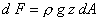(5.11)

and the force acts in a direction normal to the area dA. The components of the force dF in x, y and z directions are

	(5.12a)
	(5.12b)
	(5.13c)

Where l, m and n are the direction cosines of the normal to dA. The components of the surface element dA projected on yz, xz and xy planes are, respectively

	(5.13a)
	(5.13b)
	(5.13c)

Substituting Eqs (5.13a-5.13c) into (5.12) we can write

	(5.14a)
	(5.14b)
	(5.14c)

Therefore, the components of the total hydrostatic force along the coordinate axes are

	(5.15a)
	(5.15b)
	(5.15c)

where z_c is the z coordinate of the centroid of area A_x and A_y (the projected areas of curved surface on yz and xz plane respectively). If z_p and y_p are taken to be the coordinates of the point of action of F_x on the projected area A_x on yz plane, , we can write

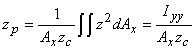
	(5.16a)
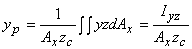	(5.16b)

where I_yy is the moment of inertia of area A_x about y-axis and I_yz is the product of inertia of A_x with respect to axes y and z. In the similar fashion, z_p^' and x _p^' the coordinates of the point of action of the force F_y on area A_y, can be written as

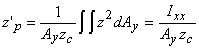
	(5.17a)
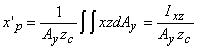	(5.17b)

where I_xx is the moment of inertia of area A_y about x axis and I_xz is the product of inertia of A_y about the axes x and z.

We can conclude from Eqs (5.15), (5.16) and (5.17) that for a curved surface, the component of hydrostatic force in a horizontal direction is equal to the hydrostatic force on the projected plane surface perpendicular to that direction and acts through the centre of pressure of the projected area. From Eq. (5.15c), the vertical component of the hydrostatic force on the curved surface can be written as

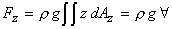(5.18)

where is the volume of the body of liquid within the region extending vertically above the submerged surface to the free surfgace of the liquid. Therefore, the vertical component of hydrostatic force on a submerged curved surface is equal to the weight of the liquid volume vertically above the solid surface of the liquid and acts through the center of gravity of the liquid in that volume.