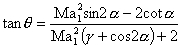Fig 41.6 Normal and oblique Shock in front of an Obstacle
Fig 41.7 Two dimensional Oblique Shock
Sometimes, a design is done in such a way that an oblique shock is allowed instead of a normal shock. The losses for the case of oblique shock are much less than those of normal shock.This is the reason for making the nose angle of the fuselage of a supersonic aircraft small.
|
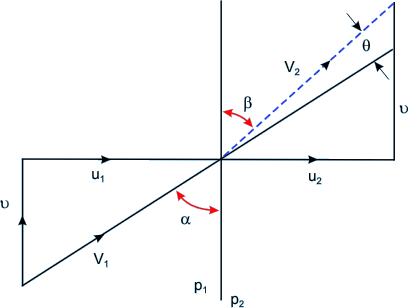
 (parallel to the shock) is superimposed. The change across shock front is determined in the same way as for the normal shock. The equations for mass, momentum and energy conservation , respectively, are
(parallel to the shock) is superimposed. The change across shock front is determined in the same way as for the normal shock. The equations for mass, momentum and energy conservation , respectively, are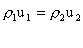
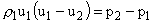
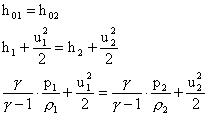
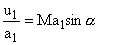
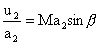
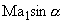 and
and
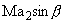 in place of
in place of
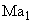 and
and
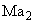 , we obtain
, we obtain 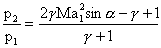
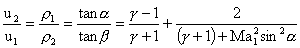
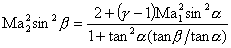
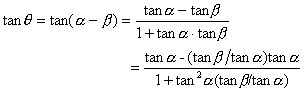
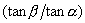 from Eq. (41.20), we get the relation
from Eq. (41.20), we get the relation