Integrating Eq. (38.35) between states 1 and 2,
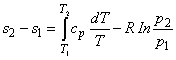 |
(38.36) |
If
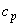 is a variable, we shall require gas tables; but for constant is a variable, we shall require gas tables; but for constant
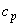 , we obtain the analytic expression , we obtain the analytic expression
In a similar way, starting with Eq. (38.31) and making use of the relation
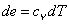 the change in entropy can also be written as the change in entropy can also be written as
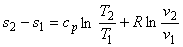 |
(38.38) |
|