Constant and Variable Density Solution

Constant Density Solution

The explicit functional relationship of hydrostatic pressure p with z can be obtained by integrating the Eq. (3.14).

For an incompressible fluid, the density r is constant throughout. Hence the Eq. (3.14) can be integrated and expressed

as

(3.15)

where C is the integration constant.

If we consider an expanse of fluid with a free surface, where the pressure is defined as p = p₀ ,which is equal to atmospheric pressure.

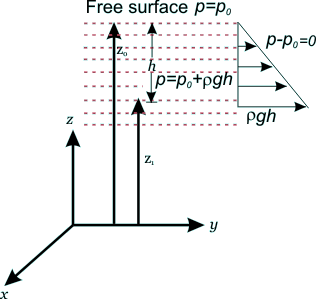
Fig 3.4 Pressure Variation in an Incompressible Fluid at rest with a Free Surface

Eq. (3.15) can be written as,

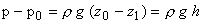
(3.16a)

Therefore, Eq. (3.16a) gives the expression of hydrostatic pressure p at a point whose vertical depression from the free surface is h.

Similarly,

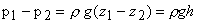
(3.16b)

Thus, the difference in pressure between two points in an incompressible fluid at rest can be expressed in terms of the vertical distance between the points. This result is known as Torricelli's principle, which is the basis for differential pressure measuring` devices. The pressure p₀ at free surface is the local atmospheric pressure.

Therefore, it can be stated from Eq. (3.16a), that the pressure at any point in an expanse of a fluid at rest, with a free surface exceeds that  of the local atmosphere by an amount rgh, where h is the vertical depth of the point from the free surface.

Variable Density Solution: As a more generalised case, for compressible fluids at rest, the pressure variation at rest depends on how the fluid density changes with height z and pressure p. For example this can be done for special cases of "isothermal and non-isothermal fluids"