Fundamental Equation of Fluid Statics

The fundamental equation of fluid statics describes the spatial variation of hydrostatic pressure p in the continuous mass of a fluid.

Derivation:

Consider a fluid element at rest of given mass with volume V and bounded by the surface S.

Fig 3.3 External Forces on a Fluid Element at Rest

The fluid element stays at equilibrium under the action of the following two forces

• The Resultant Body Force

(3.9)

: element of volume : mass of the element : body Force per unit   mass acting on the   elementary volume

• The Resultant Surface Force

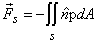(3.10)

dA : area of an element of surface 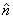  : the unit vector normal to      the elemental surface,taken      positive when directed outwards

Using Gauss divergence theorem, Eq (3.10) can be written as

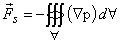(3.11)

  Click here to see the derivation

For the fluid element to be in equilibrium , we have

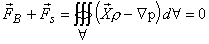(3.12)

The equation is valid for any volume of the fluid element, no matter how small, thus we get

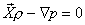
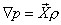	(3.13)

This is the fundamental equation of fluid statics.