|
Losses and Friction Factors
- Over a finite length l , the head loss
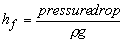 (26.11) (26.11)
Combining Eqs (26.10) and (26.11), we get
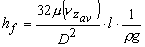 |
|
or 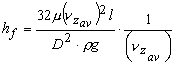 |
(26.12) |
- On the other hand, the head loss in a pipe flow is given by Darcy-Weisbach formula as
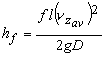 |
(26.13) |
where "f" is Darcy friction factor . Equations (26.12) and (26.13) yield
which finally gives 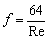 , where , where 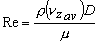 is the Reynolds number. is the Reynolds number.
- So, for a fully developed laminar flow, the Darcy (or Moody) friction factor is given by
Alternatively, the skin friction coefficient for Hagen-Poiseuille flow can be expressed by
With the help of Eqs (26.9b) and (26.9c), it can be written
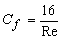 |
(26.14b) |
The skin friction coefficient Cf is called as Fanning's friction factor . From comparison of Eqs (26.14a) and (26.14b), it appears
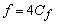 |
|
- For fully developed turbulent flow, the analysis is much more complicated, and we generally depend on experimental results. Friction factor for a wide range of Reynolds number (104 to 108) can be obtained from a look-up chart . Friction factor, for high Reynolds number flows, is also a function of tube surface condition. However, in circular tube, flow is laminar for Re ≤ 2300 and turbulent regime starts with Re ≥ 4000.
- The surface condition of the tube is another responsible parameter in determination of friction factor.
- Friction factor in the turbulent regime is determined for different degree of surface-roughness
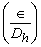 of the pipe, where of the pipe, where 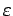 is the dimensional roughness and Dh is usually the hydraulic diameter of the pipe . is the dimensional roughness and Dh is usually the hydraulic diameter of the pipe .
- Friction factors for different Reynolds number and surface-roughness have been determined experimentally by various investigators and the comprehensive results are expressed through a graphical presentation which is known as Moody Chart after L.F. Moody who compiled it.
- The hydraulic diameter which is used as the characteristic length in determination of friction factor, instead of ordinary geometrical diameter, is defined as
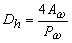 |
(26.15) |
where Aw is the flow area and Pw is the wetted perimeter .
- Kinetic energy correction factor ,
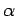 The kinetic energy associated with the fluid flowing with its profile through elemental area The kinetic energy associated with the fluid flowing with its profile through elemental area 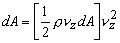 and the total kinetic energy passing through per unit
time and the total kinetic energy passing through per unit
time 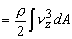 . .
- This can be related to the kinetic energy due to average velocity(
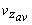 ), through a correction factor, α as ), through a correction factor, α as 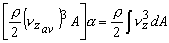
or 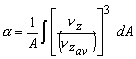 |
|
- Here, for Hagen-Poiseuille flow,
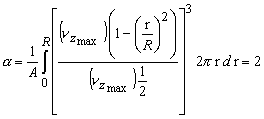 |
(26.16) |
|