|
Hagen Poiseuille Flow
- Consider fully developed laminar flow through a straight tube of circular cross-section as in Fig. 26.3. Rotational symmetry is considered to make the flow two-dimensional axisymmetric.
- Let us take z-axis as the axis of the tube along which all the fluid particles travel, i.e.
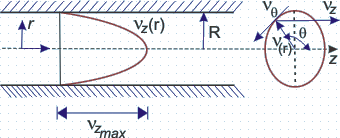
Fig 26.3 - Hagen-Poiseuille flow through a pipe
- Now, from continuity equation, we obtain
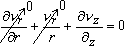 [ For rotational symmetry, [ For rotational symmetry, 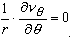 ] ] |
|
which means 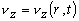
- Invoking
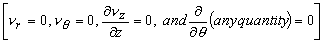 in the in the
Navier-Stokes equations, we obtain
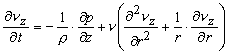 (in the z-direction) (in the z-direction) |
(26.3) |
- For steady flow, the governing equation becomes
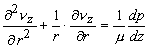 |
(26.4) |
The boundary conditions are- (i) At r = 0, 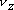 is finite and (ii) r = R, is finite and (ii) r = R, 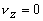 yields yields
- Equation (26.4) can be written as

- At r =0,
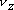 is finite which means A should be equal to zero and at r = R, is finite which means A should be equal to zero and at r = R, 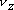 = 0 yields = 0 yields
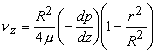 |
(26.5) |
- This shows that the axial velocity profile in a fully developed laminar pipe flow is having parabolic variation along r.
- At r = 0, as such,
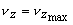
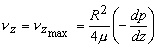 |
(26.6a) |
- The average velocity in the channel,
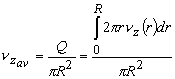 |
|
or, 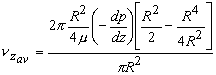 |
|
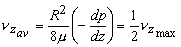
|
(26.6b) |
or 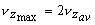 |
(26.6c) |
- Now, the discharge (Q) through a pipe is given by
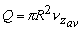 |
(26.7) |
or, 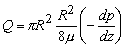 [From Eq. 26.6b] [From Eq. 26.6b] |
|
or 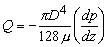 |
(26.8) |
|