Chapter 8 : Viscous Incompressible Flows
Lecture 25 :


A general way of deriving the Navier-Stokes equations from the basic laws of physics.

  • Consider a general flow field as represented in Fig. 25.1.

  • Imagine a closed control volume, within the flow field. The control volume is fixed in space and the fluid is moving through it. The control volume occupies reasonably large finite region of the flow field.

  • A control surface , A0 is defined as the surface which bounds the volume .

  • According to Reynolds transport theorem, "The rate of change of momentum for a system equals the sum of the rate of change of momentum inside the control volume and the rate of efflux of momentum across the control surface".

  • The rate of change of momentum for a system (in our case, the control volume boundary and the system boundary are same) is equal to the net external force acting on it.

        Now, we shall transform these statements into equation by accounting for each term,

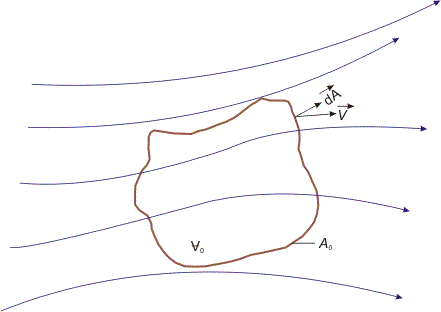
FIG 25.1 Finite control volume fixed in space with the fluid moving through it

  • Rate of change of momentum inside the control volume

 

 

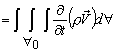   (since t is independent of space variable) (25.1)
  • Rate of efflux of momentum through control surface

 

 

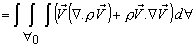(25.2)
  • Surface force acting on the control volume
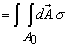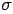 ( is symmetric stress tensor )  

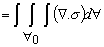(25.3)
  • Body force acting on the control volume
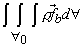(25.4)

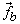in Eq. (25.4) is the body force per unit mass.

  • Finally, we get,

 
 

or

or,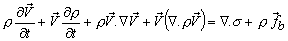     

  
or 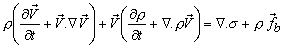     (25.5)

We know that 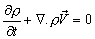is the general form of mass conservation equation (popularly known as the continuity equation), valid for both compressible and incompressible flows.

  • Invoking this relationship in Eq. (25.5), we obtain
 

 

or 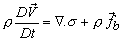      (25.6)
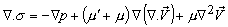(25.8)
From Stokes's hypothesis we get, 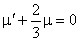(25.9)

Invoking above two relationships into Eq.( 25.6) we get

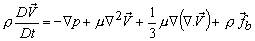(25.10)

This is the most general form of Navier-Stokes equation.