|
Nine Scalar Quantities of Stress System - Stress Tensor
The set of nine components of stress tensor can be described as
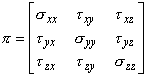 |
(24.12) |
-
The stress tensor is symmetric,
-
This means that two shearing stresses with subscripts which differ only in their sequence are equal. For example 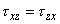
- Considering the equation of motion for instantaneous rotation of the fluid element (Fig. 24.1) about y axis, we can write
where 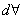 =dxdydz is the volume of the element, =dxdydz is the volume of the element, 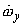 is the angular acceleration is the angular acceleration
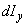 is the moment of inertia of the element about y-axis is the moment of inertia of the element about y-axis
- Since
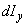 is proportional to fifth power of the linear dimensions and is proportional to fifth power of the linear dimensions and 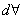 is proportional to the third power of the linear dimensions, the left hand side of the above equation and the second term on the right hand side vanishes faster than the first term on the right hand side on contracting the element to a point. is proportional to the third power of the linear dimensions, the left hand side of the above equation and the second term on the right hand side vanishes faster than the first term on the right hand side on contracting the element to a point.
- Hence, the result is
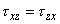
From the similar considerations about other two remaining axes, we can write
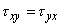
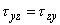
which has already been observed in Eqs (24.2a), (24.2b) and (24.2c) earlier.
- Invoking these conditions into Eq. (24.12), the stress tensor becomes
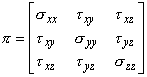 |
(24.13) |
- Combining Eqs (24.10), (24.11) and (24.13), the resultant surface force per unit volume becomes
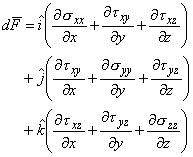 |
(8.14) |
- As per the velocity field,
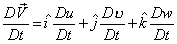 |
(24.15) |
By Newton's law of motion applied to the differential element, we can write
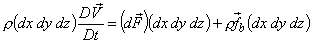
or, 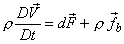
Substituting Eqs (24.15), (24.14) and (24.6) into the above expression, we obtain
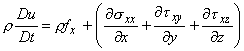 |
(24.16a) |
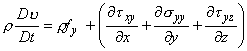 |
(24.16b) |
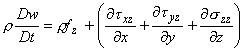 |
(24.16c) |
Since 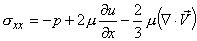
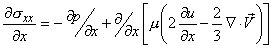
Similarly others follow.
- So we can express
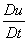 , , 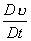 and and 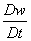 in terms of field derivatives, in terms of field derivatives,
- These differential equations are known as Navier-Stokes equations.
- At this juncture, discuss the equation of continuity as well, which has a general (conservative) form
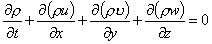 |
(24.18) |
- In case of incompressible flow ρ = constant. Therefore, equation of continuity for incompressible flow becomes
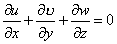 |
(24.19) |
- Invoking Eq. (24.19) into Eqs (24.17a), (24.17b) and (24.17c), we get
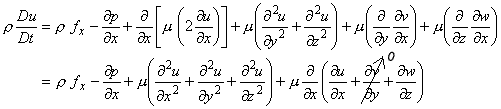
Similarly others follow
Thus,
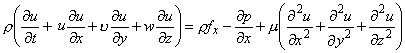
|
(24.20a) |
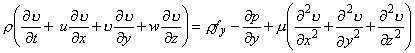
|
(24.20b) |
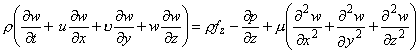 |
(24.20c) |
|